Home

Note e aggregati orizzontali¶

  • Introduzione
  • Aggregati
  • Strutture monodiche
  • Terminologia
  • Domande sospese
  • Rappresentazioni informatiche
    • Codice
      • Note
      • Beam
      • Tuplet
      • Line
      • Modifiche
    • Musica
      • Note e pause
      • Staff
      • Varibili
      • Legature e travature
      • Tuplet
      • Line
    • Suono
In [ ]:
import os
import sys

path = os.path.abspath('rappresenta')
sys.path.append(path)                     
from main import *

Introduzione ¶

Possiamo considerare una nota musicale come la minima unità semantica di un linguaggio musicale.

Nella sua forma minima è determinata da un'altezza e da una durata.

All'ìnterno di una struttura musicale anche le pause sono considerate note (unità semantiche) senza altezza.

No description has been provided for this image

Nel suo aspetto semiografico è composta da:

  1. coda
  2. gambo
  3. testa
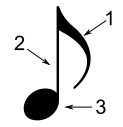
No description has been provided for this image
In [4]:
a = PNote(90, 0.5, 127)

Una nota può essere anche un suono qualsiasi senza doversi limitare alle altezze ordinate in una scala accordata con un sistema più o meno temperarto.

Aggregati ¶

Così come per i numeri a più cifre ($1.000.000$) e le parole binarie in matematica o con i byte (8 bit) in informatica anche in musica le note sono aggregate in gruppi (beams) per una più immediata lettura da parte dell'interprete.

Generalmente hanno come durata di riferimento il beat o suoi multipli e sono riconducibili alle tipologie di pulsazioni precedentemente illustrate.

No description has been provided for this image

Anche i gruppi irregolari come le terzine sono generalmente aggregate im questo modo.

No description has been provided for this image

Notaimo come graficamente le code siano sostituiti da linee orizzontali che raggruppano le linee dei gambi

Gruppi regolari ed irregolari possono essere aggregati.

No description has been provided for this image

Strutture monodiche ¶

Prestiamo attenzione in quanto gli aggregati sono elementi pratico-teorici da non confondere con gli incisi musicali che tratteremo in seguito.

Infatti così come nel linguaggio i fonemi (le più piccole unità linguistiche distintive) possono essere aggregati in morfemi (i più piccoli elementi dotati di significato) per formare le parole anche le note possono essere aggregate in incisi.

No description has been provided for this image
In [8]:
altezze = [0,      67,   67,   67, 63] 
durate  = [0.25, 0.25, 0.25, 0.25,  2]

voce1 = PSeq(altezze, durate)

voce1.start()
voce1.join()

Terminologia ¶

  • Nota musicale - minima unità semantica di un linguaggio musicale qualsiasi.
  • Pausa - come la nota senza il parametro dell'altezza.
  • Gambo e Coda - simboli grafici che definiscono la durata di una nota.
  • Testa - simbolo grafico che definisce l'`altezza di una nota e per alcuni valori anche la durata.
  • Aggregati musicali - insiemi o collezioni orizzontali di note.
  • Gruppi regolari - suddivisioni ritmiche per due e suoi multipli dell'intero.
  • Gruppi irregolari - suddivisioni ritmiche per 3,5,7,11,13,17, etc. e loro multipli dell'intero.
  • inciso musicale - aggregato musicale che assume una funzione semantica all'interno di un brano.
  • Travature - modalitá di raggruppamento di aggregati musicali.
  • Linea melodica - sequenza orizzontale di aggregati musicali.
  • Sistema musicale - Staff o pentagramma.

Domande sospese ¶

  • Realizzare l'esercizio compositivo illustrato nel paragrafo dedicato al suono o uno simile con materiali scelti da voi.
  • Argomentare le scelte effettuate nella ricomposizione in un'ottica semantica.
  • Realizzare un frammento di partitura in Lilypond e argomentare le scelte grafico-simboliche adottate.

Rappresentazioni informatiche ¶

Codice ¶

Il concetto di nota e di aggregato si prestano particolarmente ala rappresentazione attraverso il paradigma della programmazione orientata agli oggetti (OOP) nonchè alla ricerca di punti in comune tra linguaggi informatici e linguaggi musicali.

Cominciamo dal formalizzare alcune caratteristiche musicali:

  • una nota è un elemento singolo
  • può aggregarsi in collezioni come beat (suddivisioni regolari) e tuplet (suddivisioni irregolari).
  • note, beat e tuplet possono aggregarsi ulteriormente e formare delle line (sequenze più lunghe)

Nel modulo che stiamo utilizzando c'è una classe per ognumo di questi elementi.

Note ¶

Rappresenta una singola nota musicale attraverso la quale possiamo costruire sequenze e accordi.

Accetta tre attributi:

  • diatonic_pitch - un'istanza di DiatonicPitch(oct, 'pitch').
  • base_duration - la durata base senza eventuali punti e può essere:
    • un'istanza di Duration(1, 8)
    • per i valori standard:
      • 'w': 1/1
      • 'h': 1/2
      • 'q': 1/4
      • 'e': 1/8
      • 's': 1/16
      • 't': 1/32
      • 'x': 1/64
  • num_dots - numero di eventuali punti.

Se ci sono dei punti possiamo ottenere la durata totale invocando il metodo duration.

In [7]:
n1 = Note(DiatonicPitch(4, 'c'),  Duration(1,4))
n2 = Note(DiatonicPitch(5, 'f#'), 'q', 1)

print(n1)
print(n2)

[C:4<1/4>-(1/4)] off=0 f=1
[F#:5<1/4@>-(3/8)] off=0 f=1

Osserviamo il formato nel quale sono riportati i parametri.

Possiamo ottenere (getter) le singole informazioni attraverso metodi dedicati.

In [9]:
print('Pitch: {}'.format(n2.diatonic_pitch))  
print('Durata base: {}'.format(n2.base_duration))  
print('Numero di punti: {}'.format(n2.num_dots) ) 
print('Durata: {}'.format(n2.duration))  

print('Offset: {}'.format(n2.relative_position))  
print('Fattore: {}'.format(n2.contextual_reduction_factor))  

Pitch: F#:5
Durata base: 1/4
Numero di punti: 1
Durata: 3/8
Offset: 0
Fattore: 1

Possiamo anche modificare dinamicamente (setter) gli stessi parametri.

In [11]:
n2.diatonic_pitch = DiatonicPitch(6, 'd') 
n2.offset         = Duration(1,4)

print('Pitch: {}'.format(n2.diatonic_pitch))  
print('Offset: {}'.format(n2.offset)) 

Pitch: D:6
Offset: 1/4

Il parametro legato al fattore di riscalaggio non ha molto senso per le note ma lo avrà negli aggregati.

Beam ¶

E'un contenitore he rappresenta un aggregato di note con ritmi regolari.

Accetta una collezione di:

  • Note()
  • Tuplet()
  • Beam()

Ogni nuova istanza incapsulata riduce le durate di 1/2.

In [13]:
n1 = Note(DiatonicPitch(4, 'c'), 'q')
n2 = Note(DiatonicPitch(4, 'd'), 'e')
n3 = Note(DiatonicPitch(4, 'e'), 'e')
n4 = Note(DiatonicPitch(4, 'f'), 'q')

b1 = Beam([n1,n2,n3])
print(b1)

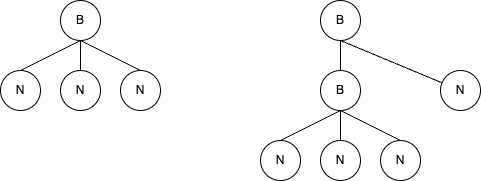
b2 =  Beam([b1, n4]) # b_1 è ridotto di 1/2
print(b2)

Beam(Dur(1/2)Off(0)f=1)[
  [C:4<1/4>-(1/4)] off=0 f=1
  [D:4<1/8>-(1/8)] off=1/4 f=1
  [E:4<1/8>-(1/8)] off=3/8 f=1
]
Beam(Dur(1/2)Off(0)f=1)[
  Beam(Dur(1/4)Off(0)f=1/2)[
  [C:4<1/8>-(1/8)] off=0 f=1/2
  [D:4<1/16>-(1/16)] off=1/8 f=1/2
  [E:4<1/16>-(1/16)] off=3/16 f=1/2
]
  [F:4<1/4>-(1/4)] off=1/4 f=1
]
No description has been provided for this image
No description has been provided for this image

Tuplet ¶

Come il precedente ma per tempi irregolari.

Accetta come attributi:

  • unit_duration è il valore della singola unità di tempo.
  • unit_duration_factor è il numero di unit_duration.
    • La moltiplicazione dei due valori precedenti definisce la durata totale dell'aggregato.
    • Le durate specificate in Note() valgono solo come proporzione e sono riscalate in base al valore precedente.
  • una collezione di:
    • Note()
    • Tuplet()
    • Beam().
In [15]:
n1 = Note(DiatonicPitch(4, 'c'), 'e')         # durata = eight
n2 = Note(DiatonicPitch(4, 'd'), 'e')
n3 = Note(DiatonicPitch(4, 'e'), 'e')

t1 = Tuplet(Duration(1, 4), 2, [n1,n2,n3]) # durata = half

print(t1)

Tuplet(1/4x2Dur(1/2)Off(0)f=4/3)[
  [C:4<1/6>-(1/6)] off=0 f=4/3
  [D:4<1/6>-(1/6)] off=1/6 f=4/3
  [E:4<1/6>-(1/6)] off=1/3 f=4/3
]
No description has been provided for this image

Anche in questo caso dobbiamo fare attenzione al beaming e al nesting delle strutture.

Line ¶

Rappresenta una linea di elementi come potrebbe essere una voce di una partitura.

Possiamo utilizzarla per incollare tra loro diverse strutture come gli incisi musicali.

Accetta una collezione di:

  • Note()
  • Tuplet()
  • Beam(0
  • Line()
No description has been provided for this image
No description has been provided for this image
In [17]:
t1 = Tuplet(Duration(1, 4), 2, [Note(DiatonicPitch(4, 'c'), 'q'),
                                Note(DiatonicPitch(4, 'd'), 'q'),
                                Note(DiatonicPitch(4, 'e'), 'q')]) 
n1 = Note(DiatonicPitch(4, 'f'), 'q')
b1 = Beam([Beam([Beam([Note(DiatonicPitch(4, 'g'), 'q'),
                       Note(DiatonicPitch(4, 'a'), 'q')]),
                 Beam([Beam([Note(DiatonicPitch(4, 'b'), 'q'),
                             Note(DiatonicPitch(4, 'c'), 'q'),
                             Note(DiatonicPitch(4, 'd'), 'q'),
                             Note(DiatonicPitch(4, 'e'), 'q')])
                       ])
                ])
          ])

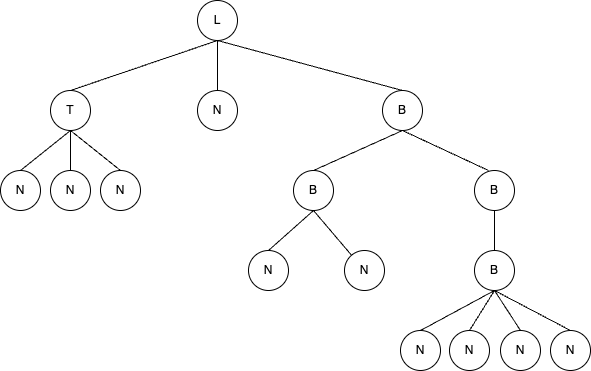
l1 = Line([t1, n1, b1])    # Incorpora anche le strutture delle celle precedenti
print(l1)

Line(Dur(1)Off(0)f=1)[
  Tuplet(1/4x2Dur(1/2)Off(0)f=2/3)[
  [C:4<1/6>-(1/6)] off=0 f=2/3
  [D:4<1/6>-(1/6)] off=1/6 f=2/3
  [E:4<1/6>-(1/6)] off=1/3 f=2/3
]
  [F:4<1/4>-(1/4)] off=1/2 f=1
  Beam(Dur(1/4)Off(3/4)f=1)[
  Beam(Dur(1/4)Off(0)f=1/2)[
  Beam(Dur(1/8)Off(0)f=1/4)[
  [G:4<1/16>-(1/16)] off=0 f=1/4
  [A:4<1/16>-(1/16)] off=1/16 f=1/4
]
  Beam(Dur(1/8)Off(1/8)f=1/4)[
  Beam(Dur(1/8)Off(0)f=1/8)[
  [B:4<1/32>-(1/32)] off=0 f=1/8
  [C:4<1/32>-(1/32)] off=1/32 f=1/8
  [D:4<1/32>-(1/32)] off=1/16 f=1/8
  [E:4<1/32>-(1/32)] off=3/32 f=1/8
]
]
]
]
]

Modifiche ¶

Anche per Beam(), Tuplet() e Line() possiamo:

  • conoscere la durata totale.
In [19]:
print(l1.duration) 

1
  • richiamare gli elementi uno alla volta per indice (partendo da 0).
In [21]:
items = l1.sub_notes                    # una lista degli elementi che compongono il beam
print(items[0])                         # possiamo richiamarli per indici

Tuplet(1/4x2Dur(1/2)Off(0)f=2/3)[
  [C:4<1/6>-(1/6)] off=0 f=2/3
  [D:4<1/6>-(1/6)] off=1/6 f=2/3
  [E:4<1/6>-(1/6)] off=1/3 f=2/3
]
  • aggiungere elementi alla fine (append)
In [23]:
l1.append(Note(DiatonicPitch(4, 'f'), 'q')) # Aggiunta una nota alla fine
print(l1)

Line(Dur(5/4)Off(0)f=1)[
  Tuplet(1/4x2Dur(1/2)Off(0)f=2/3)[
  [C:4<1/6>-(1/6)] off=0 f=2/3
  [D:4<1/6>-(1/6)] off=1/6 f=2/3
  [E:4<1/6>-(1/6)] off=1/3 f=2/3
]
  [F:4<1/4>-(1/4)] off=1/2 f=1
  Beam(Dur(1/4)Off(3/4)f=1)[
  Beam(Dur(1/4)Off(0)f=1/2)[
  Beam(Dur(1/8)Off(0)f=1/4)[
  [G:4<1/16>-(1/16)] off=0 f=1/4
  [A:4<1/16>-(1/16)] off=1/16 f=1/4
]
  Beam(Dur(1/8)Off(1/8)f=1/4)[
  Beam(Dur(1/8)Off(0)f=1/8)[
  [B:4<1/32>-(1/32)] off=0 f=1/8
  [C:4<1/32>-(1/32)] off=1/32 f=1/8
  [D:4<1/32>-(1/32)] off=1/16 f=1/8
  [E:4<1/32>-(1/32)] off=3/32 f=1/8
]
]
]
]
  [F:4<1/4>-(1/4)] off=1 f=1
]
  • realizzare un time stretching (apply_factor)
In [25]:
l1.apply_factor(1/2)                        
print(l1)

Line(Dur(5/8)Off(0)f=0.5)[
  Tuplet(1/4x2Dur(1/4)Off(0)f=0.3333333333333333)[
  [C:4<1/12>-(1/12)] off=0 f=0.3333333333333333
  [D:4<1/12>-(1/12)] off=1/12 f=0.3333333333333333
  [E:4<1/12>-(1/12)] off=1/6 f=0.3333333333333333
]
  [F:4<1/8>-(1/8)] off=1/4 f=0.5
  Beam(Dur(1/8)Off(3/8)f=0.5)[
  Beam(Dur(1/8)Off(0)f=0.25)[
  Beam(Dur(1/16)Off(0)f=0.125)[
  [G:4<1/32>-(1/32)] off=0 f=0.125
  [A:4<1/32>-(1/32)] off=1/32 f=0.125
]
  Beam(Dur(1/16)Off(1/16)f=0.125)[
  Beam(Dur(1/16)Off(0)f=0.0625)[
  [B:4<1/64>-(1/64)] off=0 f=0.0625
  [C:4<1/64>-(1/64)] off=1/64 f=0.0625
  [D:4<1/64>-(1/64)] off=1/32 f=0.0625
  [E:4<1/64>-(1/64)] off=3/64 f=0.0625
]
]
]
]
  [F:4<1/8>-(1/8)] off=1/2 f=0.5
]
  • realizzare un retrogrado (reverse).
In [27]:
l1.reverse()                                 
print(l1)

Line(Dur(5/8)Off(0)f=0.5)[
  [F:4<1/8>-(1/8)] off=0 f=0.5
  Beam(Dur(1/8)Off(1/8)f=0.5)[
  Beam(Dur(1/8)Off(0)f=0.25)[
  Beam(Dur(1/16)Off(0)f=0.125)[
  Beam(Dur(1/16)Off(0)f=0.0625)[
  [E:4<1/64>-(1/64)] off=0 f=0.0625
  [D:4<1/64>-(1/64)] off=1/64 f=0.0625
  [C:4<1/64>-(1/64)] off=1/32 f=0.0625
  [B:4<1/64>-(1/64)] off=3/64 f=0.0625
]
]
  Beam(Dur(1/16)Off(1/16)f=0.125)[
  [A:4<1/32>-(1/32)] off=0 f=0.125
  [G:4<1/32>-(1/32)] off=1/32 f=0.125
]
]
]
  [F:4<1/8>-(1/8)] off=1/4 f=0.5
  Tuplet(1/4x2Dur(1/4)Off(3/8)f=0.3333333333333333)[
  [E:4<1/12>-(1/12)] off=0 f=0.3333333333333333
  [D:4<1/12>-(1/12)] off=1/12 f=0.3333333333333333
  [C:4<1/12>-(1/12)] off=1/6 f=0.3333333333333333
]
]
In [29]:
a = Note(60, 'e', 1)
print(a)

[60<1/8@>-(3/16)] off=0 f=1

Musica ¶

In Lilypond ci sono diversi comandi che riguardano gli argomenti di questo capitolo.

In [14]:
! /Applications/Frescobaldi.app/Contents/MacOS/Frescobaldi

qt.qpa.fonts: Populating font family aliases took 124 ms. Replace uses of missing font family "Monospace" with one that exists to avoid this cost.

Note ¶

Il concetto teorico di nota appena espresso si riflette anche nel linguaggio impiegato dal Lilypond in quanto la minima unità semantica di questo linguaggio informatico è definita porprio dall'ínsieme di altezza_durata.

In [ ]:
\version "2.24.3"
\language "english"

\relative c' {c4 d f g}

Potremo specificare tutti gli altri elementi grafici solo dopo aver indicato questi due parametri.

Ad esempio aggiungiamo delle dinamiche fisse.

In [ ]:
\relative c' {c8\p d e f g a b\mf c e1\sfz}

Pause¶

Anche in questo caso possiamo pensare le pause come una nota senza la specifica dell'altezza che sostituiamo con la lettera r (rest).

In [ ]:
\relative c' {c8 d r g r b c d}

Se vogliamo uno spazio vuoto senza il simbolo delle pause utilizziamo la lettera s (space).

In [ ]:
\relative c' {c8 d s g s b c d}

Staff ¶

Finora abbiamo specificato il contenuto musicale includendolo tra parentesi graffe senza preoccuparci troppo di altre caratteristiche di una partitura.

Cominciamo a formalizzare il pensiero sia informatico che musicale specificando un rigo musicale al quale successivamente daremo ulteriori caratteristiche.

In [ ]:
\new Staff {
            \relative c' {c4 d f g}
            }

Variabili (beam) ¶

Proseguiamo il processo di formalizzazione specificando gli aggregati musicali (Beaming) attraverso variabili.

Questa formalizzazione può essere sia informatica che musicale.

In [ ]:
seqa =  {c4 d8 f g2}              % Variabili
seqb =  {g8 a b c a4 g4}
seqc =  {g2 c,}

\new Staff {
            \relative c'     \seqa % Richiama le variabili più volte (line)
            \relative c''    \seqb
            \relative c'''  \seqc
            }

Legature e travature ¶

Negli aggregati musicali possiamo specoificare ulteriori elementi musciali come i diversi tipi di legature:

  • di valore - aumentano la durata di una o più note sommando i valori tra loro. Si utilizza il simbolo tilde (~)
In [ ]:
\relative c'{c4~ c8 d16 e f4~ f8 g~ g1}
  • di portamento - legato inteso come espressione. Si utilizza la parentesi tonda sia relata alla nota di apertura che a quella di chiusura.
In [ ]:
\relative c'{c4~( c8 d16 e) f4~( f8 g~ g1)}
  • di frase - indicano un fraseggio più ampio. Si utilizza la parentesi tonda preceduta da uno slash sia relata alla nota di apertura che a quella di chiusura.
In [ ]:
\relative c'{c4~(\( c8 d16 e) f4~( f8 g~ g1)\)}

Possiamo anche modificare le travature di default raggruppando in modo diverso gli agglomerati musicali. La sintassi è la stessa delle legature di portamento ma con parentesi quadre.

In [ ]:
\relative c'{c8 d e[ f g] a [b c d] c d e f g[ f e]}

Dovrebbe essere chiara ora la struttura sintattica della nota: altezza_durata_altri_elementi.

Tuplet ¶

I gruppi irregolari sono specificati attraverso il comando \tuplet frazione { musica }.

In [ ]:
 \relative c' {
               \tuplet 3/2 { c8 e g }
               a g
               \tuplet 5/4 { g16 a b c  d }
               \tuplet 3/2 { e4 d8}
               c1
               }

Line ¶

Attraverso le variabili possiamo anche formalizzare il pensiero musicale di una linea melodica ripetendo incisi.

In [ ]:
seqa =  {c4 d8 f g2}              % Variabili
seqb =  {g8 a b c a4 g4}
seqc =  {g2 c,}
seqd =   \tuplet 3/2 { c8 e g }

\new Staff {
            \relative c'    \seqd % Richiama le variabili più volte (line)
            \relative c''   \seqd
            \relative c'''  \seqc
            \relative c'    \seqa
            \relative c''   \seqb
            \relative c''   \seqa
            r2
            }

Suono ¶

Per quanto riguarda l'aspetto più strettamente legato alle note sonore (oggetti sonopri) possiamo:

  • scaricare e importare in Audacity il soundfile con il frammento sonoro di B.Parmegiani.
  • identificare, isolare, e tagliare in frammenti i singoli elementi sonori che possiamo identificare come note.
  • riordinare (ricomporre) sulla stessa traccia nuovi agglomerati sonori eventualmente modificandone altezza, durata e ampiezza.
  • salvare i singoli agglomerati come soundfile per poi ricomporli in nuovi agglomerati di agglomerati.

N.B. Utilizzare una singola traccia mono.

Brevi indicazioni operative per la realizzazione in Audacity.

  • Tagliare un soundfile:
    • posizionare il cursore nel punto desiderato.
    • $\rightarrow$ Modifica $\rightarrow$ Clip Audio $\rightarrow$ Dividi (oppure command + I)
  • Selezionare un frammento: click sulla parte superiore.
  • Selezionare più frammenti: click e trascina.
  • Salvare una selezione come soundfile:
    • selezionare (anche parti di file o più files).
    • $\rightarrow$ File $\rightarrow$ Esporta Audio $\rightarrow$ Esporta intervallo $\rightarrow$ selezione corrente.
  • Fade in - out:
    • selezionare con il cursore lo spazio di fade (inizio o fine del file).
    • $\rightarrow$ Effetti $\rightarrow$ Dissolvenza $\rightarrow$ Dissolvenza in entrata (o in uscita).

Le eventuali modifiche di altezza, durata e ampiezza le abbiamo già illustrate nei capitoli precedenti.