Temperamenti¶
import os
import sys
path = os.path.abspath('rappresenta')
sys.path.append(path)
from main import *
Introduzione¶
Possiamo definire con il termine teoria musicale le regole attraverso le quali sono organizzati i parametri del suono nei diversi linguaggi musicali.
Queste regole sono poi applicate nella composizione, nell'analisi e nell'interpretazione del testo musicale.
In quasi tutte le tradizioni musicali passate, presenti e probabilmente future uno degli aspetti principali è dato dalla definizione dei rapporti tra diverse altezze.
In questo corso ci occuperemo principalmente delle regole afferenti alla tradizione musicale occidentale, cominciamo dunque con il definire:
- scala pitagorica - costruita sui suoni naturali derivati dal monocordo.
- scala naturale - costruita sui rapporti dei parziali armonici.
- scala cromatica - costruita sui 12 semitoni con temperamento equabile.
Faremo riferimento a due diversi modi di rappresentare le altezze:
- Tono diatonico - rapresenta un altezza musicale senza distinzione d'ottava (La).
- Pitch diatonico - rapresenta un altezza musicale con distinzione d'ottava (La4).
Scala pitagorica ¶
La scala pitagorica rappresenta un modo di organizzare un insieme di altezze in modo consonante basandosi sui rapporti matematici (frazioni o ratio) che descrivono le suddivisioni delle vibrazioni di una corda.
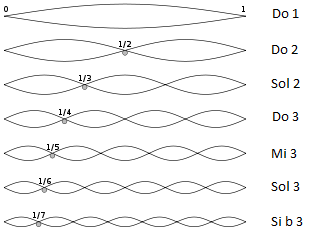
La scala pitagorica è relativa in quanto si basa su un altezza di riferimento che corrisponde alla frequenza data dalle vibrazioni della corda intera (1:1).
Tutti gli altri rapporti (pitch diatonici) sono relati a questa altezza (root pitch).
Vedremo come le rappresentazioni relative e/o assolute siano una costante in ambito musicale e sonoro.
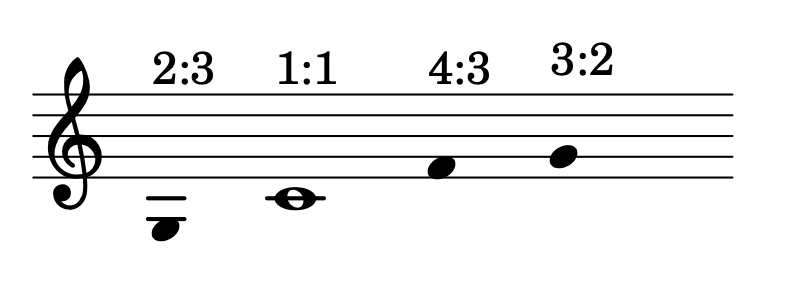
I rapporti fondamentali considerati consonanti da Pitagora sui quali costruire l'intera scala sono due:
- 2:1 - ottava superiore.
- 3:2 - quinta perfetta superiore.
Prendiamo in considerazione anche il rapporto inverso della quinta perfetta:
- 2:3 - quarta perfetta inferiore.

root = 261 # Do centrale in Hertz
fatto = np.array([1/2, 2/3, 1/1, 3/2, 2/1])
freqs = root * fatto
print(np.round(fatto,3))
print(np.round(freqs))
[0.5 0.667 1. 1.5 2. ] [130. 174. 261. 392. 522.]
Partendo da questo principo possiamo costruire la scala moltiplicando 7 volte la frequenza dell'altezza di riferimento per 3/2 in senso ascendente e altre 7 per 2/3 in senso discendente.
| 2/3 | <-- | Root | --> | 3/2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SOLb | REb | LAb | MIb | SIb | FA | DO | SOL | RE | LA | MI | SI | FA# |
| 64/729 | 32/243 | 16/81 | 8/27 | 4/9 | 2/3 | 1 | 3/2 | 9/4 | 27/8 | 81/16 | 243/32 | 729/64 |
| 0.087 | 0.131 | 0.197 | 0.296 | 0.444 | 0.666 | 1 | 1.5 | 2.25 | 3.375 | 5.062 | 7.593 | 11.390 |
root = 400 # Do centrale
giu = np.array([(2/3)**6, (2/3)**5, (2/3)**4, (2/3)**3, (2/3)**2, (2/3)**1])
su = np.array([(3/2)**1, (3/2)**2, (3/2)**3, (3/2)**4, (3/2)**5, (3/2)**6])
fatto = np.concatenate((giu, [1], su))
freqs = root * fatto
print(list(np.round(fatto,3)))
print(list(np.round(freqs)))
[0.088, 0.132, 0.198, 0.296, 0.444, 0.667, 1.0, 1.5, 2.25, 3.375, 5.062, 7.594, 11.391] [35.0, 53.0, 79.0, 119.0, 178.0, 267.0, 400.0, 600.0, 900.0, 1350.0, 2025.0, 3038.0, 4556.0]
E' quello che in tempi moderni viene definito il circolo delle quinte.
Come risulta evidente tutte le moltiplicazioni per 2:3 a scendere e tutte quelle oltre il rapprto 9:4 a salire escono dal range 1:2 (ottava).
Per riportarle correttamente all'interno di questo ambito dobbiamo trovare il multiplo appropriato per le ratio:
- sequenza ascendente moltiplicare per $(\frac{1}{2})^{n}$ dove $n$ è il numero di ottava che eccede.
- sequenza discendente moltiplicare per $2^{n}$ dove $n$ è il numero di ottava che eccede.
Ad esempio per ottenere la quarta superiore basterà moltiplicare $2/3 \cdot 2^{1} = 4/3$
root = 261 # Do centrale
fatto = 2/3 * 2**1
freq = root * fatto
print(fatto)
print(freq)
1.3333333333333333 348.0
Nella seguente tabella lo sviluppo di questo procedimento
| 2/3 | <-- | Root | --> | 3/2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SOLb | REb | LAb | MIb | SIb | FA | DO | SOL | RE | LA | MI | SI | FA# |
| 64/729 | 32/243 | 16/81 | 8/27 | 4/9 | 2/3 | 1 | 3/2 | 9/4 | 27/8 | 81/16 | 243/32 | 729/64 |
| 128/729 | 64/243 | 32/81 | 16/27 | 8/9 | 4/3 | 9/8 | 27/16 | 81/32 | 243/64 | 729/128 | ||
| 256/729 | 128/243 | 64/81 | 32/27 | 16/9 | 81/64 | 243/128 | 729/256 | |||||
| 512/729 | 256/243 | 128/81 | 729/512 | |||||||||
| 1024/729 |
def ratio_su(esp3, esp2):
return (3 ** esp3) / (2 ** esp2) # 3**n / 2**n
def ratio_giu(esp2, esp3):
return (2 ** esp2) / (3 ** esp3) # 2**n / 3**n
esp2 = 0
esp3 = 0
for m in range(1,7):
esp3 = esp3 + 1
esp2 = esp2 + 1
ratio = ratio_giu(esp2, esp3) # Calcola la ratio
if ratio < 1: # Se supera l'ottava aumenta il denominatore
esp2 = esp2 + 1
ratio = ratio_giu(esp2, esp3)
print('%4i:%4i ratio = %8f' % (2**esp2, 3**esp3, ratio))
esp2 = 0
esp3 = 0
print('-------------------------')
print('%4i:%3i ratio = %8f' % (1, 1, 1))
print('-------------------------')
for m in range(1, 7):
esp3 = esp3 + 1
esp2 = esp2 + 1
ratio = ratio_su(esp3, esp2) # Calcola la ratio
if ratio > 2: # Se supera l'ottava aumenta il denominatore
esp2 = esp2 + 1
ratio = ratio_su(esp3, esp2)
print('%4i:%3i ratio = %8f' % (3**esp3, 2**esp2, ratio))
4: 3 ratio = 1.333333 16: 9 ratio = 1.777778 32: 27 ratio = 1.185185 128: 81 ratio = 1.580247 256: 243 ratio = 1.053498 1024: 729 ratio = 1.404664 ------------------------- 1: 1 ratio = 1.000000 ------------------------- 3: 2 ratio = 1.500000 9: 8 ratio = 1.125000 27: 16 ratio = 1.687500 81: 64 ratio = 1.265625 243:128 ratio = 1.898438 729:512 ratio = 1.423828
Notiamo che gli estremi non ordinati ovvero il Fa# ed il Sol b non hanno la stessa ratio e dunque un'intonazione differente.
Possiamo dunque definire la scala pitagorica una scala aperta in quanto il circolo non si chiude.
Se ordiniamo le ratio in modo crescente otteniamo una scala di 12 semitoni.

Scala naturale¶
Una possibile soluzione trovata dai teorici della musica nel corso dei secoli consiste nel costruire le ratio secondo i suoni che costituiscono la serie degli armonici naturali.
E' chiamata anche intonazione giusta o pura.
Stabiliamo un'altezza di riferimento in Hertz (root pitch) e la moltiplichiamo per numeri interi ottenendo la sequenza dei parziali armonici (Teorema di Fourier).

root = 400
harm = root * np.array([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16])
print(" 1 2 3 4 5 6 7 8 9 10 11 12 13:8 14 15 16")
print(" 1:1 2:1 3:2 2:1 5:4 3:2 7:4 2:1 9:8 5:4 11:8 3:2 13:8 7:4 15:8 2:1")
print(list(harm))
1 2 3 4 5 6 7 8 9 10 11 12 13:8 14 15 16 1:1 2:1 3:2 2:1 5:4 3:2 7:4 2:1 9:8 5:4 11:8 3:2 13:8 7:4 15:8 2:1 [400, 800, 1200, 1600, 2000, 2400, 2800, 3200, 3600, 4000, 4400, 4800, 5200, 5600, 6000, 6400]
Riportiamo i valori risultanti nell'ambito dell'ottava dividendo anche in questo caso i valori per $2^{n}$ eliminando eventuali doppioni secondo un principio di arbitrarietà.

Quella illustrata è una possibile scala naturale cromatica (12 semitoni all'interno dell'ottava).
Scala cromatica ¶
Un altro modo di costruire una scala cromatica è il sistema denominato temperamento equabile (well-tempered tuning).
Questo metodo consiste nel definire il rapporto tra due semitoni consecutivi con $2^{1/12}$ o meglio $1.059$ e calcolare i successivi in modo che per tutte le ottave ci sia coerenza di intonazione evitando i problemi riscontrati nella scala pitagorica e in quelle naturali.
Questo sistema a volte è chiamato 12-EDO oppure 12-TET in quanto suddivide l'ottava in 12 parti uguali.
for i in range(13):
ratio = 2**(i/12)
print(ratio)
1.0 1.0594630943592953 1.122462048309373 1.189207115002721 1.2599210498948732 1.3348398541700344 1.4142135623730951 1.4983070768766815 1.5874010519681994 1.681792830507429 1.7817974362806785 1.8877486253633868 2.0
Possiamo ora computare la differenza con la scala pitagorica determinando il valore del comma pitagorico.
def ratio_su(esp3, esp2):
return (3 ** esp3) / (2 ** esp2)
esp2 = -1
esp3 = -1
for m in range(0, 13):
esp3 = esp3 + 1
esp2 = esp2 + 1
ratio = ratio_su(esp3, esp2)
if ratio > 2:
esp2 = esp2 + 1
ratio = ratio_su(esp3, esp2)
diff = (np.log2(ratio) - 1 / 12) * 1200 # differenza con temperamento equabile
diff = np.remainder(diff, 100)
print('%6i:%6i ratio = %8f +%4.2f cents' % (3**esp3, 2**esp2, ratio, diff))
1: 1 ratio = 1.000000 +0.00 cents
3: 2 ratio = 1.500000 +1.96 cents
9: 8 ratio = 1.125000 +3.91 cents
27: 16 ratio = 1.687500 +5.87 cents
81: 64 ratio = 1.265625 +7.82 cents
243: 128 ratio = 1.898438 +9.78 cents
729: 512 ratio = 1.423828 +11.73 cents
2187: 2048 ratio = 1.067871 +13.69 cents
6561: 4096 ratio = 1.601807 +15.64 cents
19683: 16384 ratio = 1.201355 +17.60 cents
59049: 32768 ratio = 1.802032 +19.55 cents
177147:131072 ratio = 1.351524 +21.51 cents
531441:524288 ratio = 1.013643 +23.46 cents
Il comma pitagorico è dato dall'ultimo valore (la differenza tra gli estremi del circolo delle quinte).
Il temperamento equabile è il meno raffinato tra quelli illustrati ma meglio si adatta all'evoluzione tecnica nella costruzione degli strumenti musicali e alla conseguente evoluzione dei linguaggi musicali.
Si è affermato lentamente come riferimento in Europa a partire dalla fine del 1.500.
Ma perchè 12 note e non 10 o 16?
Almeno due motivi:
- per ottimizzare le caratteristiche della scala naturale (evoluzione storica).
- è il più piccolo temperamento che contiene:
- tutti e sette i toni di base
- più intervalli consonanti rispetto a quelli dissonanti.
La scala fondata sul temperamento equabile assume un altezza di riferimento (root pitch) ma a differenza dalle altre può estendersi verso l'alto e verso il basso.
Questo la rende neutra in quanto qualsiasi altezza può essere quella di riferimento e ci porta a due domande:
- esiste una frequenza minima e una massima?
- possiamo definire una frequenza centrale di riferimento dalla quale computare tutti i semitoni?
Partiamo dalla risposta alla seconda domanda: il La diapason (A4) a 440 Hz stabilito con la risoluzione europea numero 71 del 30 giugno 1971.
Prima di allora la frequenza di riferimento era estremamente variabile a seconda del luogo e paese.
La risposta alla prima domanda invece dipende dalla caratteristiche (range) dello strumento musicale (o voce) impiegato.
Scale moderne occidentali¶
Se osserviamo in modo differente una scala cromatica neutra e se cerchiamo di unire il concetto di diatonico e cromatico otteniamo qualla che possiamo definire la scala diatonica che suddivide un'ottava cromatica in 7 toni diatonici base che corrispondono ai nomi delle note (C, D, E, F, G, A, B) e 5 toni diatonici alterati che corrispondono agli stessi con le alterazioni o accidenti.
c#-db d#-eb f#-gb g#-ab a#-bb
C | D | E F | G | A | B
0 1 2 3 4 5 6 7 8 9 10 11

Le alterazioni standard sono:
- bb = doppio bemolle ( -2 semitoni)
- b = bemolle ( -1 semitono)
- # = diesis ( +1 semitono)
- ## = doppio diesis ( +2 semitoni)
Possiamo notare come per ogni un singolo tasto dei toni aumentati corrispondano due note (approfondiremo più avanti la ragione).
Questi si chiamano toni enamonici e possiamo definirli attraverso delle equivalenze.
D# == Eb == Fbb
2(+1) 4(-1) 5(-2)
3 3 3
Ricordiamo come nel temperamento equabile corrispondono alla stessa frequenza mentre in altri temperamenti no.
dia = [60, 62, 64,65, 67, 69, 71 ] # Scala diatonica
alt = [ 61, 63, 66, 68, 70 ] # Gradi alterati
cro = [60,61,62,63,64,65,66,67,68,69,70,71] # Scala cromatica
d = [dia, alt, cro]
for i in d:
for b in i:
PNote(b, 0.5, 127)
time.sleep(1)
Linea del tempo¶
Grecia antica (e culture musicali extraeuropee) la coesistenza di temperamenti e scale diverse era naturale anzi utile ai fini espressivi (un`accordatura calante fornisce un senso di tristezza o calma mentre una crescente di brillantezza o agitazione(.
Nell'Europa medioevale i teorici descrissero solamente la scala e il temperamanto Pitagorico avendo conseguenze pratiche anche sull'espressività artistica.
Nel corso del XV secolo nelle composizioni polifoniche venivano utilizzati sempre più frequentemente gli intervalli di terza ma la terza maggiore nella scala pitagorica è poco consonante. Diventa prassi comune temperare le quinte (accordarle calanti) per cercare di ottenere terze maggiori più consonanti cioè più vicine al rapporto 4/5.
Nel corso del XVI secolo è largamente attestata dai trattatisti la pratica del temperamento mesotonico (tutte le quinte ugualmente calanti). Anche questo temperamento però non era chiuso e produceva una quinta molto aperta (quinta del lupo).
A partire dal 1558 trovò applicazione pratica la scala naturale quando il teorico Gioseffo Zarlino ne svicerò le caratteristiche nello scritto "Le istitutioni harmoniche" proseguendo la teoria fisico-numerica della scuola pitagorica.
Il principale problema musicale del temperamento naturale è dato dal fatto che se un brano si sviluppa in un unica tonalità (definita dal root pitch) viene rispettato il principio di consonanza ma se dovesse contenere delle modulazioni tutti i rapporti verrebbero meno e risulterebbe stonato.
Un esempio di cromatismo nell'espressione musicale che poneva grossi problemi di intonazione.
Il tedesco Andreas Werckmeister nel cercare di correggere gli inconvenienti dei temperamenti esistenti per favorire le nuove necessità espressive scoprì nel 1691 un'accordatura ciclica che conteneva cinque quinte mesotoniche e sette quinte giuste (pitagoriche).
Probabilmente era questo il temperamento impiegato da J.S.Bach per il Clavicembalo ben temperato.
Per questo e altri motivi come l'evoluzione delle tecniche costruttive degli strumenti musicali i teorici della musica occidentale cominciarono a cercare un'altra possibile soluzione che consiste nel mantenere la stessa ratio per due altezze ascendenti consecutive definendo in questo modo la scala cromatica con temperamento equabile.
Nel corso del XVIII e XIX teorici e musicisti cominciano a considerare i vantaggi del temperamento equabile superiori agli svantaggi dovuti all'assenza di intervalli giusti rendendolo di fatto il temperamento standard fino ai nostri giorni.
Cominciamo ad osservare come nel corso di una tradizione musicale gli aspetti teorici, linguistici, espressivi, percettivi, emotivi, pratici e antropologici si intrecciano stimolando vicendevolmente un evoluzione complessa.
Terminologia¶
- Temperamento - sistemi per ricavare rapporti di altezze tipicamente all'interno di un'ottava.
- pitagorico
- naturale, giusto o puro
- equabile
- Consonanza - per gli antichi gli intervalli di quarta, quinta e ottava (ratio 4:3, 3:2, 2:1).
- Circolo delle quinte - successione di quinte perfette fino a coprire il totale cromatico ritornando al primo tono diatonico.
1 2 3 4 5 6 7 8 9 10 11 12 Do Sol Re La Mi Si Fa# Do# Sol# Re# La# Mi#
- Cent: centesimo di semitono equabile o milleduecentesimo di ottava. La misura dell'intervallo tra due frequenze ($f1<f2$) in cent è su scala logaritmica e possiamo calcolarla attraverso la formula $1200 \cdot log_{2}(f2 / f1)$.
- Comma: differenza di frequenza che si ha a seconda del temperamento.
- Comma pitagorico - la differenza frequenziale tra gli estremi del circolo delle quinte (+ 23.46 cents).
- Root note (nota perno) - tono cromatico al quale assegnare indice 0 per calcolare il rapporto con altri toni.
- Alterazioni (accidenti) - diesis, bemolle, doppio diesis, doppio bemolle +/- 1 o 2 semitoni.
- Tono diatonico - rapresenta un altezza musicale senza distinzione d'ottava come La#.
- Pitch diatonico - rapresenta un altezza musicale con distinzione d'ottava come La4#.
- Toni diatonici base - corrispondono ai nomi della note (sette).
- Toni diatonici alterati - corrispondono ai diesis e bemolli necessari a coprire il totale cromatico.
- Scala diatonica: scala eptatonica i cui gradi corrispondono ai toni diatonici base.
- Scala cromatica: scala dodecatonica che suddivide l'ottava in dodici semitoni che corripondono ai toni diatonici base più i toni diatonici alterati.
Domande sospese¶
L'evoluzione dei temperamnenti nella tradizione musicale occidentale ha sempre seguito il susseguirsi delle sensibilità espressive nelle varie epoche e l'evoluzione delle tecniche di costruzione degli strumenti musicali.
Pitagorico
Mesotonico
Naturale
Equabile
I diversi temperamenti hanno fortemente caratterizzato le diverse epoche e i diversi linguaggi musicali in modo profondo e strettamente legato alle specifiche regole e caratteristiche musicali ma...
a quale significato semiotico possono rimandare l'ascoltatore contemporaneo?
- maggiore o minore nitidezza/opacità dell'immagine sonora?
- collocazione percettiva del testo musicale in un epoca del passato più o meno precisa?
- maggiore o minore attivazione emotiva?
- ...
quali implicazioni sono relative al processo di astrazione simbolica insito nell'evoluzione storica dei sistemi di temperamento nella tradizione occidentale?
Prendiamo come esempio la scala pitagorica sappiamo che è aperta e questo ci pone di fronte ad alcune riflessioni:
- teoricamente (pensiero astratto) - Fa# è uguale a Sol b come rappresentazione di un altezza all'interno del sistema di organizzazione (codice), inoltre entrambi i simboli potrebbero definire lo stesso tono ma assumono significati differenti.
- percettivamente (mondo freale) - in fisica non sono lo stesso suono e non sono percepiti come uguali dal ricevente assumendo dunque due significati diversi.
I diversi temperamenti possono dare carattere emotivo o affettivo a un brano musicale?
Possiamo paragonare l'effetto percettivo dei diversi temperamenti a quello che ai nostri giorni chiamiamo sound?
Rappresentazione informatica¶
Per formalizzare alcuni concetti musicali e per illustrare le principali caratteristiche e probematiche relate alla programmazione di sistemi acustici e musicali utilizziamo:
- una libreria di Python organizzata secondo il paradigma della programmazione orientata ad oggetti basata sul lavoro di Donald P. Pazel.
- un software di videoscrittura (Lilypond).
- una DAW (Audacity).
Codice ¶
Oltre alle rappresentazioni musicali presentate nel paragrafo dedicato ci sono altre forme proprie dei linguaggi informatici attraverso cui definire le altezze.
Prendiamo come esempio della tradizione musicale occidentale odierna il range del pianoforte che si estende secondo un temperamento equabile da 4 ottave sotto A4 fino a 4 ottave sopra per un totale di 88 semitoni (A0 - C8).
Siccome la scala cromatica temperata è una scala neutra se vogliamo mantenere un'organizzazione per rapporto d'ottava dobbiamo definire una partizione cromatica alla quale assegnare dei numeri come indici o rapporti intervallari.

int = np.array([0,1,2,3,4,5,6,7,8,9,10,11]) # intervalli
root = 60
pitch = root + int
for i in pitch:
PNote(i, 0.2, 127)
Successivamente posiamo assegnare una locazione cromatica ovvero altri indici che identificano le ottave assegnando all'ottava che contiene A4 l'indice 4 e di conseguenza la prima sarà contraddistinta dall'indice 0.

Questa definizione ci permette di definire l'altezza di una nota nelle seguenti ulteriori forme proprie di molti linguaggi informatici:
- (ottava, indice) - collezione di dati binari (int).
- 'ottava:indice' - stringa
- posizione assoluta o distanza cromatica - int
int = np.array([0,1,2,3,4,5,6,7,8,9,10,11]) # intervalli
oct = np.array([0,1,2,3,4,5,6,7,8]) # ottave
for i in oct:
root = 12 * i
for i in int:
PNote(i + root, 0.1, 127)
ChromaticScale
E' una classe statica con un utilizzo limitato in quanto serve esclusivamente come contenitore di dati all'interno di progetti informatici di più ampio respiro.
Contiene e rappresenta tutti i semitoni equabili da A0 a C8.
Informazioni e funzioni ottenibili invocando i metodi:
scala = ChromaticScale # Classe statica
scala_hz = scala.get_chromatic_scale((4,0),(4,5)) # Lista di frequenze da Do4 a Fa4
pitch_hz = scala.get_frequency((4,0)) # Singola frequenza (Hz)
parse = scala.parse_notation('5:2') # Parsing da stringa a collezione
idx = scala.location_to_index(parse) # (o, i) --> id
loc = scala.index_to_location(idx) # id --> (o,i)
start = scala.chromatic_start_index() # inizio assoluto dell'ambito di riferimento (A0).
end = scala.chromatic_end_index() # fine assoluto dell'ambito di riferimento (C8).
print("Hz: ", scala_hz)
print("Frq:", pitch_hz)
print("Pos:", parse)
print("Idx:", idx)
print("Loc:", loc)
print("Sta:", start)
print("End:", end)
Hz: [261.62556530059896, 277.1826309768725, 293.66476791740797, 311.1269837220814, 329.62755691287043, 349.22823143300445] Frq: 261.62556530059896 Pos: (5, 2) Idx: 62 Loc: (5, 2) Sta: 9 End: 96
DiatonicTone
Questa Classe rappresenta un tono diatonico ovvero un'altezza musicale senza distinzione di ottava.
Possiamo definire un tono diatonico in diversi modi:
- Simbolo diatonico - 'A#' - nome + alterazione. Per praticità utilizziamo i nomi delle note anglosassoni.
- Nome diatonico - solo il nome.
- Simbolo alterazione - solo l'alterazione.
- Indice diatonico - indice dei soli nomi delle note DO = 0.
- Offset alterazione - numero di semitoni da aggiungere o sottrarre.
- Offset tonale - numero di semitoni assoluti calcolato a partire da DO = 0
- Placement - offset corretto nel caso esca dall'ottava come 'B#' o 'Cb'.
Anche in questo caso possiamo effettuare diverse operazioni ed ottenere informazioni.
Vediamo le principali operazioni sulla singola istanza.
tono = DiatonicTone('Cb') # Istanza che rappresenta un tono diatonico
nome = tono.diatonic_symbol # Simbolo diatonica
parse = tono.parse('Cb') # Parsing
lettera = tono.diatonic_letter # Nome diatonico
alteraS = tono.augmentation_symbol # Simbolo alterazione
indice = tono.diatonic_index # Indice diatonico senza alterazione
offset = tono.augmentation_offset # Offset alterazione
aoffset = tono.tonal_offset # Offset tonale (0 = root)
toffset = tono.placement # Offset relativo all'ottava
print('Simbolo:', nome)
print('Parsing:', parse)
print('Nome:', lettera)
print('Alterazione:', alteraS)
print('Indice diatonico:', indice)
print('Offset alterazione:', offset)
print('Offset assoluto:', aoffset)
print('Placement:', toffset)
Simbolo: Cb
Parsing: ('C', 'b')
Nome: C
Alterazione: b
Indice diatonico: 0
Offset alterazione: -1
Offset assoluto: -1
Placement: 11
Possiamo anche utilizzare la singola istanza per ottenere informazioni su altri toni passandoli come argomenti dei rispettivi metodi.
tono = DiatonicTone('C')
enarmonici = tono.enharmonics() # Lista di suoni enarmonici per l'altezza dell'istanza
enarmonicia = tono.enharmonics_for('E') # Lista di suoni enarmonici per un tono specificato come argomento
id_2_nome = tono.get_diatonic_letter(0) # Simbolo della nota diatonica
altera = tono.augmentation(-1) # Simbolo dell'alterazione
print('Enarmonici:', enarmonici)
print('Enarmonici:', enarmonicia)
print('Nome diatonico:', id_2_nome)
print('Alterazione:', altera)
Enarmonici: ['C', 'B#', 'Dbb'] Enarmonici: ['E', 'D##', 'Fb'] Nome diatonico: C Alterazione: b
Come possiamo osservare le principali operazioni su questo parametro sono:
- definire una o più forme sintattiche per definire un parametro
- prevedere il parsing ed eventualmente un casting tra le diverse forme e tipi.
- effettuare queste operazioni con tecniche di mapping attraverso collezioni indicizzate come i dictionary.
DiatonicPitch
Questa Classe a differenza della precedente rappresenta un'altezza musicale all'interno di un'ottava definita.
Accetta due argomenti:
- numero di ottava int > 0.
- rappresentazione di un'istanza di DiatonicTone sotto forma di stringa 'Ab'
# ottava, tono
pitch = DiatonicPitch(4, 'C#')
print('Ottava:', pitch.octave)
print('Offset cromatico:', pitch.chromatic_distance) # distanza cromatica in semitoni dall'altezza più bassa = 0
print('Offset diatonico:', pitch.diatonic_distance()) # distanza diatonica dall'altezza più bassa 0
print('Parsing:', pitch.parse('C#4')) # Forma alternativa
Ottava: 4 Offset cromatico: 49 Offset diatonico: 28 Parsing: C#:4
Le classi illustrate in questo paragrafo come già accennato non servono a molto ma possiamo considerarle come mattoni con i quali costruire un sistema informatico più ampio e complesso, esattamente come ciò che rappresentano in un sistema musicale.
Musica ¶
In questo paragrafo introduciamo l'utilizzo del software Lilypond.
Un software di videoscrittura rappresenta i parametri musicali.
L'ambiente di lavoro è simile in tutti gli IDE che possiamo utilizzare sia in locale (Frescobaldi) che in remoto (Hacklily).
Apriamo Frescobaldi.
! /Applications/Frescobaldi.app/Contents/MacOS/Frescobaldi
qt.qpa.fonts: Populating font family aliases took 115 ms. Replace uses of missing font family "Monospace" with one that exists to avoid this cost.
Osserviamo come tutti sono divisi in tre parti:
- un interprete dove scrivere le istruzioni.
- una finestra dove sono riportati eventuali messaggi di errore o altro.
- una o più finestre per visualizzare l`anteprima del file pdf generato.
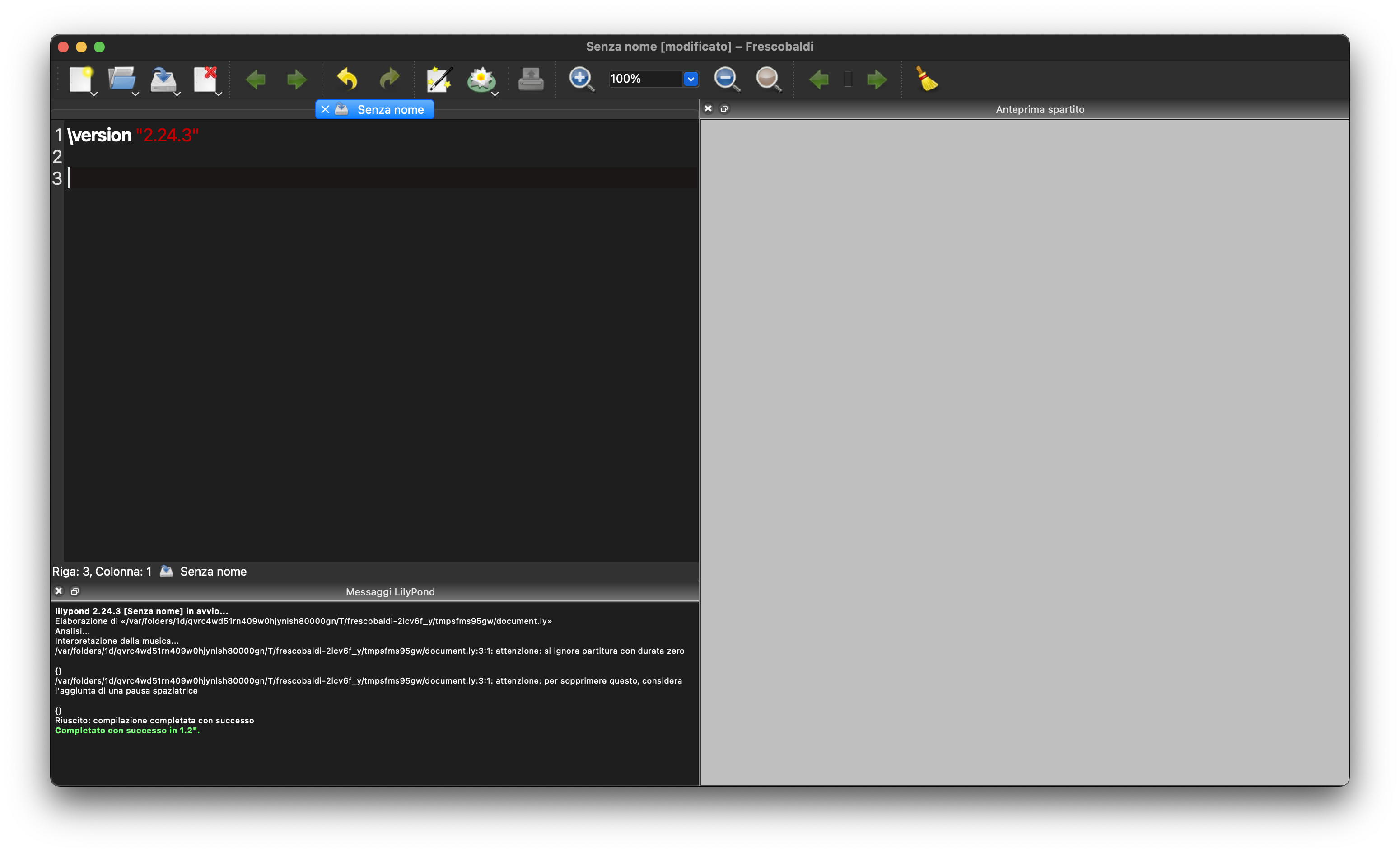
Ogni file deve cominciare con la:
- dichiarazione dlla versione corrente per consentire compatibilità future.
- lingua che vogliamo impiegare per specificare i nomi delle note (consiglio l'inglese).
\version "2.24.3"
\language "english"
Per il momento possiamo scrivere direttamente una sequenza di note diatoniche includendole tra parentesi graffe.
{a b c d e f g}
Se abbiamo impostato la compilazione automatica vedremo comparire l'anteprima dello spartito altrimenti clicchiamo sull'ìcona del fiore di loto.
Notiamo come tutte siano comprese all'interno di un'ottava, per la precisioone quella che parte da C3.
In questo caso se vogliamo cambiare ottava rispetto a quella di riferimento dobbiamo aggiungere per ogni nota
- uno o più apici (') per le ottave sopra.
- una o più virgole (,) per quelle sotto.
{a b, c' d'' e,,, f'' g,}
C'é un metodo più pratico che consiste nel relativizzare la posizione.
\relative c'{c e g c d g f d b c g e c}
Per le alterazioni aggiungiamo al nome (senza spazio) le iniziali in lingua inglese:
- f $\rightarrow$ flat (bemolle)
- s $\rightarrow$ sharp (diesis)
- ff $\rightarrow$ double flat (doppio bemolle)
- ss $\rightarrow$ double sharp (doppio diesis)
- ! $\rightarrow$ natural (bequadro)
- ? $\rightarrow$ aggiunto all'àlterazione la include tra parentesi.
Differentemente dalla teoria musicale le alterazioni valgono per le singole note e non per l'intera misura.
\relative c'{c ef g c ds? g f d b css gff e! c}
Se vogliamo omettere il metro o nascondere i gambi delle note o le linee di battuta.
\relative c'{
\omit Staff.TimeSignature
\hide Staff.Stem
\hide Staff.BarLine
c ef g c ds? g f d b css gff e! c
}
Possiamo consultare on line:
Suono ¶
In questo paragrafo introduciamo l'utilizzo del software Audacity come esempio di DAW generica.
Una DAW rappresenta i parametri acustici.
Nell'immagine l'interfaccia grafica attuale.
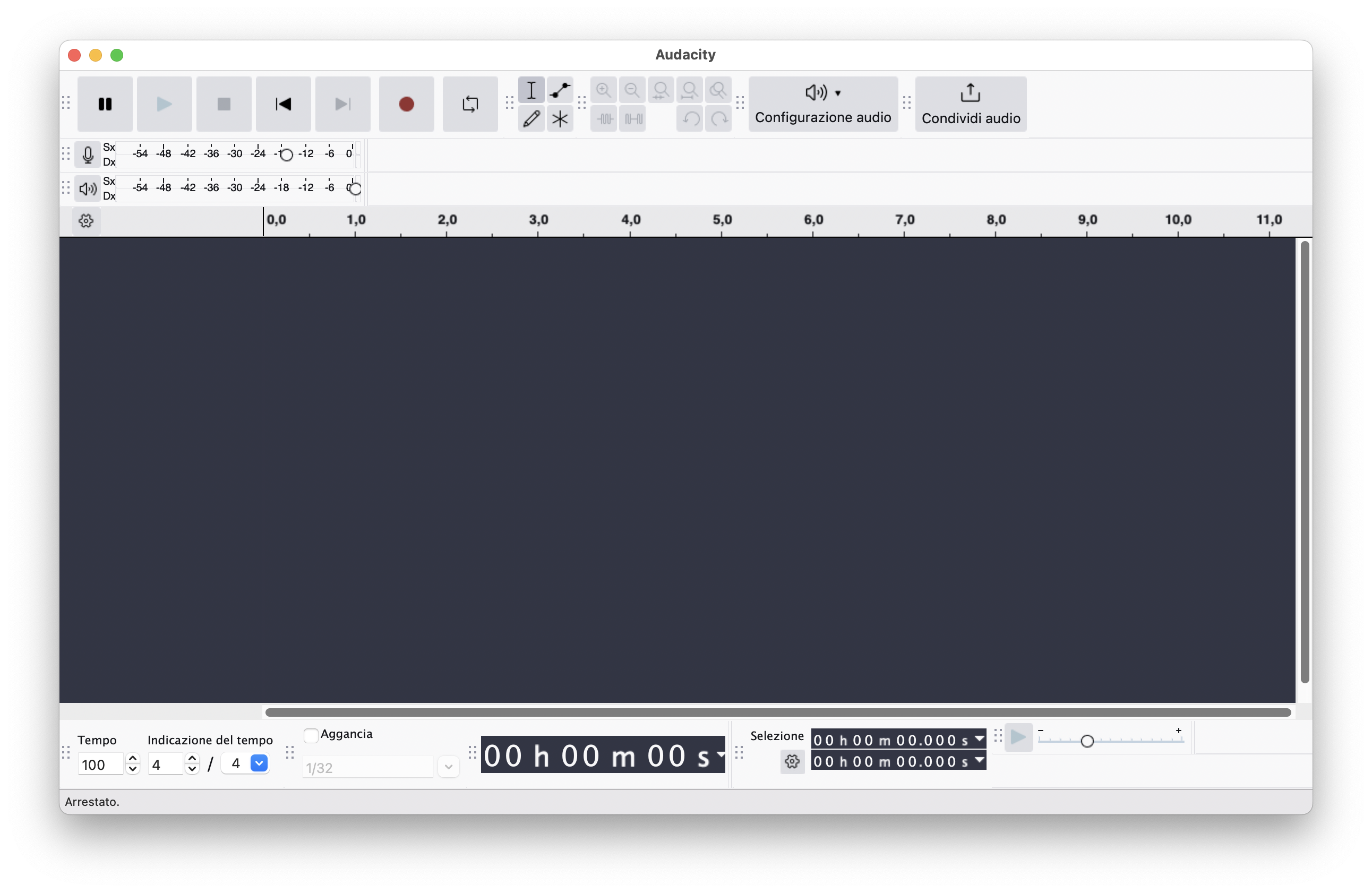
Operazioni basilari:
- collegare il software con le porte audio che vogliamo utilizzare cliccando su Configurazione audio.
- trascinare un soundfile per creare una nuova traccia audio (uno di prova a questo link).
Se vogliamo accordare la traccia su un diapason diverso oppure trasportarla:
- la selezioniamo con il mouse
- $\rightarrow$ Effetti $\rightarrow$ Intonazione e tempo $\rightarrow$ Cambia intonazione.
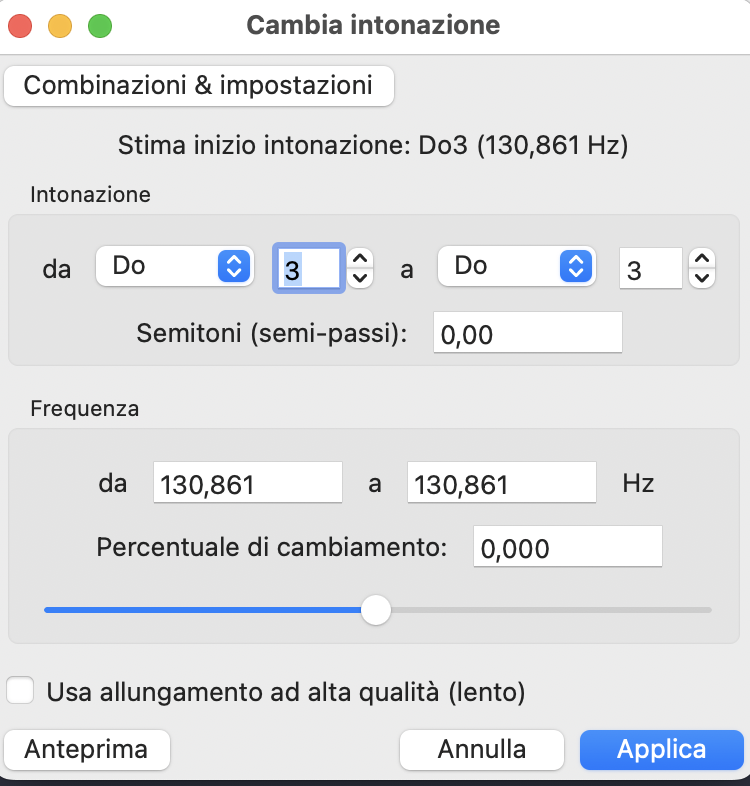
N.B. Ci sono diversi modi per compiere questa operazione.
Dopo aver configurato l'ingresso microfonico possiamo anche registrare:
- $\rightarrow$ Preferenze $\rightarrow$ Impostazioni audio $\rightarrow$ Registrazione $\rightarrow$ Canali: 1 (mono).
- $\rightarrow$ Tracce $\rightarrow$ Aggiungi nuova $\rightarrow$ Traccia mono.
- $\rightarrow$ Cliccare sull'icona Pausa.
- $\rightarrow$ Cliccare sull'icona Record.
- $\rightarrow$ Verificare il volume in ingresso.
- $\rightarrow$ Cliccare sull'icona Pausa (comincia a registrare).
- $\rightarrow$ Cliccare sull'ícona Stop per terminare la registrazione.
- $\rightarrow$ File $\rightarrow$ Esporta audio.. salva un soundfile corrispondente alla traccia.
- $\rightarrow$ File $\rightarrow$ Salva progetto salva l'intero progetto Audacity.