Cenni di Acustica, teoria e semiografia musicale¶
import os
import sys
path = os.path.abspath('music_rep_master') # Restituisce il path assoluto della cartella
sys.path.append(path) # Include la cartella nel path di lavoro
from main import * # Importa tutte le cLassi del modulo
Definizioni ¶
Acustica - Scienza che studia il suono, le sue proprietà, il suo meccanismo di formazione, propagazione, ricezione, ecc.; è una delle parti in cui didatticamente si suddivide la fisica e rientra nella meccanica intesa in senso lato.
Teoria musicale - Disciplina che considera i fondamenti della musica e ne fornisce un sistema per poterli articolare e utilizzare in un linguaggio compositivo.
Semiografia - Sistema di notazione o di scrittura abbreviata mediante segni convenzionali.
Suono, onde sonore e musica¶
Il suono è un fenomeno fisico che viene generato attraverso la produzione di onde sonore da parte di un corpo elastico messo in vibrazione chiamato sorgente sonora (strumento musicale, corde vocali, membrana di un altoparlante. etc.) che provoca piccole variazioni nella pressione atmosferica.
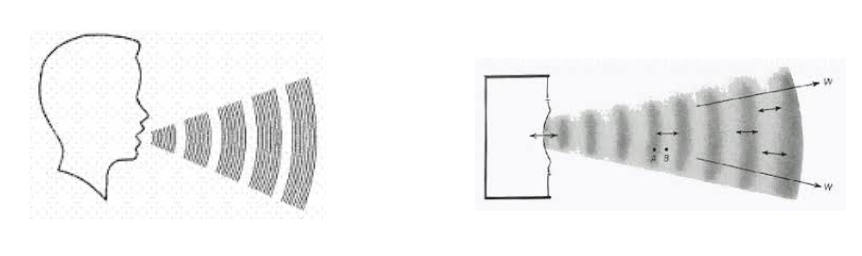
In fisica un’onda è una perturbazione che si propaga nello spazio e che può trasportare energia da un punto all’altro.
Per produrre suono la sorgente sonora deve essere immersa all’interno di un mezzo elastico che solitamente ma non necessariamente è l’aria.
Quando un'onda viaggia in un mezzo elestico la sostanza di questo mezzo è temporaneamente deformata.
Le onde sonore si propagano attraverso collisioni tra molecole vicine.
Dopo la collisione le molecole tornano indietro in direzione opposta, oscillando intorno ad una posizione quasi fissa.
Le onde sonore sono onde meccaniche longitudinali in quanto le oscillazioni sono parallele alla direzione della propagazione.
Pensiamo ai puntini più a sinistra (quelli compresi tra i limiti +/- 1) come a molecole attigue alla membrana di un altoparlante che vengono spostate attraverso la forza del suo movimento generando in questo modo un'onda sonora.
I suoni non necessitano di qualcuno che li ascolti, semplicemente esistono sulla terra.
Nel corso del suo tragitto all’interno del corpo vibrante un’onda sonora però può incontrare un apparato in grado di trasformare (ed eventualmente elaborare) l’energia sonora in energia di altra forma.
il sistema uditivo umano trasforma le variazioni di pressione atmosferica in impulsi nervosi.
un microfono trasforma le variazioni di pressione atmosferica in variazioni di tensione elettrica.

Nel primo caso le onde sonore sono recepite dai nostri sensi come inputs, stimoli che il nostro cervello interpreta come informazioni.
L'atto di ascoltare infatti è uno dei mezzi di conoscenza del mondo che ci circonda forniti dai nostri sensi.
Lo stimolo sonoro che abbiamo appena percepito è esistito nella realtà delle cose esclusivamente sotto forma di piccole variazioni della pressione atmosferica ma il nostro cervello le ha interpretate come il ruggito di un leone.
In qualità di esseri umani siamo infatti usi a generare, interpretare, dedurre, richiamare o creare nuove informazioni stimolati da informazioni esterne.
Riassumendo:
Le onde sonore sono un messaggio informativo obiettivo (fenomeno fisico - minuscole variazioni di pressione atmosferica).
Se intercettate da un essere umano sono trasdotte dai nostri sensi (apparato uditivo) sotto forma di impulsi nervosi in modo obiettivo ma non lineare e dipendente dalle caratteristiche fisiologiche della singola persona.
L'informazione proveniente dagli impusi nervosi è interpretata dal nostro cervello secondo diverse modalità.
Una definizione ridotta ai minimi termini di musica può essere:
- la musica è un qualche tipo di organizzazione dei suoni nel tempo che fornisce un qualche tipo di informazioni all'ascoltatore - ricevente.
Gli elementi che sono organizzati in un qualunque sistema musicale corripondono alle proprietà fisiche del suono:
- Altezza (frequenza)
- Dinamica (ampiezza)
- Timbro (strumentazione o tecnica di sintesi e/o elaborazione)
- Tempo (ritmo)
Ritornando a un esempio proposto nel capitolo cenni di semiotica generale:
Suono
Musica
In entrambi gli esempi possiamo misurare ed eventualmente organizzare le proprietà sonore appena esposte.
Altezza o frequenza ¶
L’altezza (o frequenza) di un suono è il parametro legato alla sensazione di gravità/acutezza che si percepisce e dipende dalle frequenze di variazione delle onde elementari che compongono l’onda sonora.
Onde periodiche ¶
Un'onda periodica è data da un fenomeno vibratorio che si ripete identico a se stesso a intervalli di tempo uguali.
- se il singolo intervallo viene misurato nel tempo è chiamato periodo (o ciclo) dell'onda e rappresentato dalla lettera T.
- se il singolo intervallo viene misurato nello spazio è chiamato lunghezza dell'onda e rappresentato dalla lettera $\lambda$ - lambda.
Possiamo rappresentare graficamente un onda attraverso un sistema di riferimento cartesiano:
- asse delle ascisse (x) = scorrere del tempo
- asse delle ordinate (y) = variazioni di pressione atmosferica
La frequenza di un suono periodico è misurata in Hertz o cps (cicli per secondo) ovvero si misura quante volte il periodo si ripete uguale in un secondo.

L'orecchio umano nelle sue condizioni ottimali percepisce suoni compresi tra 20 e 20.000 Hz.
Rappresentazioni ¶
Possiamo specificare questo parametro in tre diversi tipi di notazione simbolica:
Simboli musicali - determinano l'altezza in base alla posizione grafica in un contesto di linguaggio codificato (la scrittura musicale).
Pentagramma - cinque righi che definiscono una voce o uno strumento musicale.

Chiavi - tre simboli che definiscono un'altezza di riferimento.
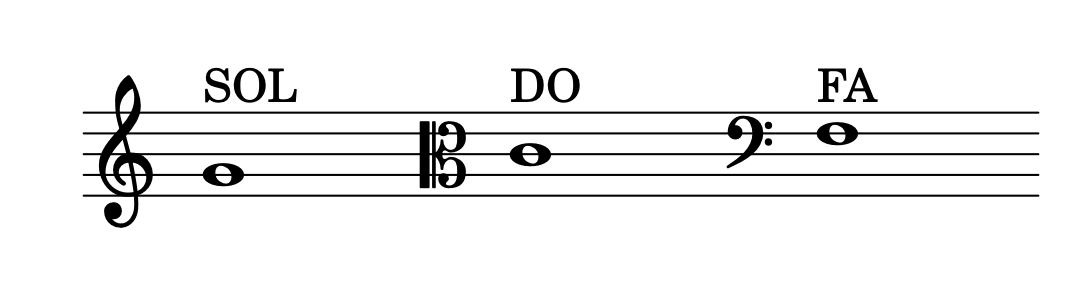
- Posizioni - spazi o righi.

- Alterazioni o accidenti - diesis, bemolle, bequadro, doppio diesis, doppio bemolle. Alterano di uno o due semitoni.
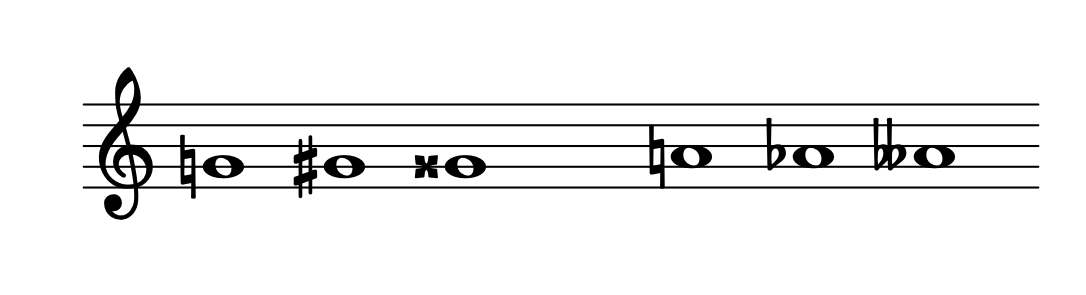
- Tagli addizionali - per le altezze che cadono al di sopra o al di sotto del pentagramma.

Simboli alfabetici - determinano l'altezza come nomi di una scala (diatonica o cromatica) o un modo Guido d'Arezzo - Inno a San Giovanni Battista (1028 ca.).


Simboli numerici - in questo caso possiamo fare un'ulteriore suddivisione in quattro diverse unità:
Gradi - determinano l'altezza come posizioni in una scala diatonica o in un modo.

Rapporti intervallari - determinano l'altezza di una scala cormatica come distanza da un'altezza di riferimento (root note) in genere definita con il valore 0.

Rappresentazioni assolute - determinano l'altezza di una attraverso simboli impiegabili facilmente in linguaggi informatici.
- Numerazione MIDI.
- Numerazione a Ottave (Giapponese, Yamaha, Encore).
- Numerazione a Ottave (Scientifica, MusicXML ed altre).
- Numerazione di Helmholtz (utilizzata comunemente negli Stati Uniti).
- Numerazione Esadecimale.
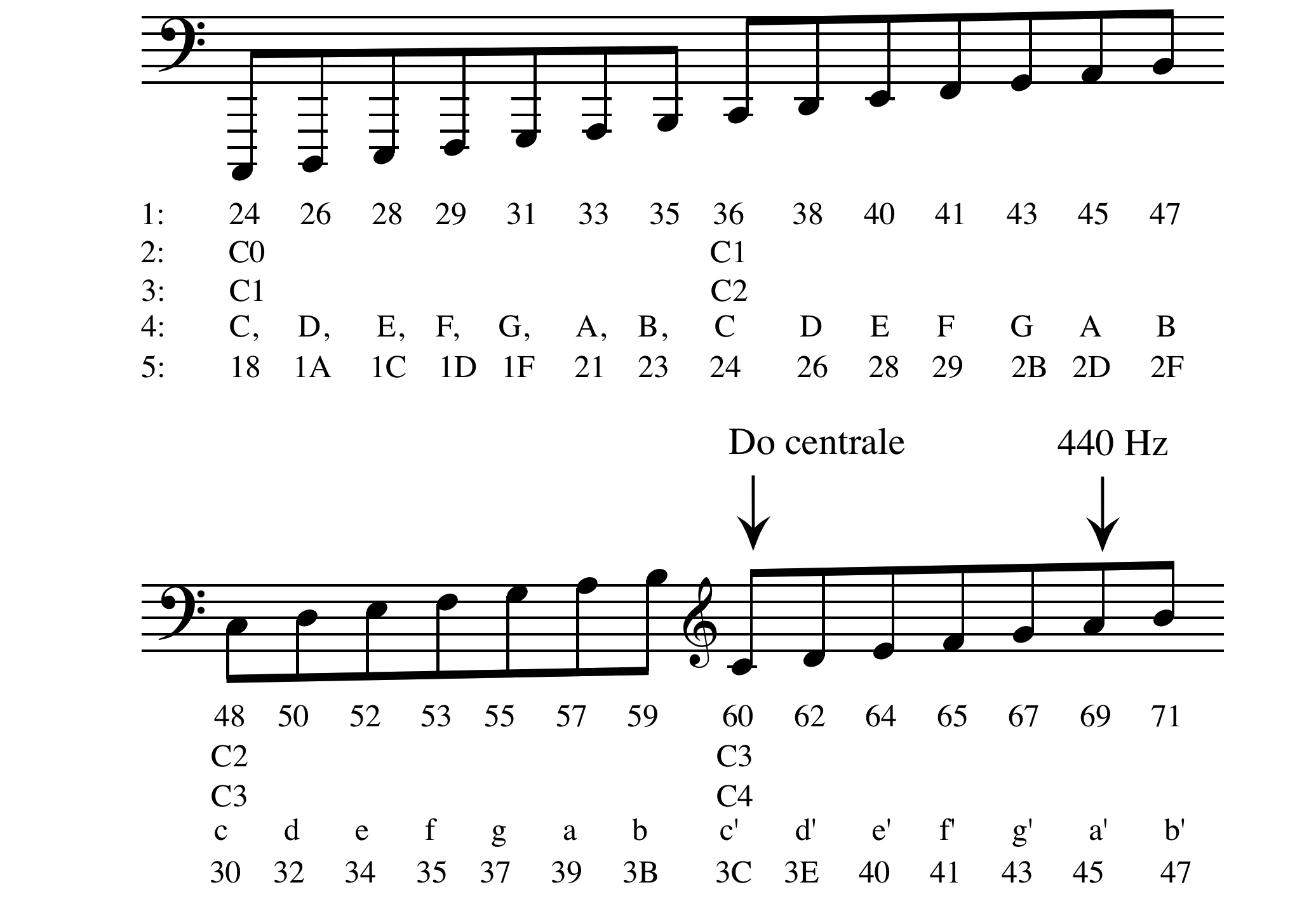
- Frequenze (Hertz) - determinano l'altezza come numero di cicli per secondo di un'onda periodica o ciclica.

Nella seguente tabella i rapporti tra alcune unità di misura appena esposte.
| Nota | MIDI | Rapporto | Frequenza (Hz) | |
|---|---|---|---|---|
| Do | 60 | $1:1$ | 261.6 | |
| Do# o Reb | 61 | $\sqrt[12]{2}$ | 277.2 | |
| Re | 62 | $\sqrt[12]{2^2}$ | 293.7 | |
| Re# o Mib | 63 | $\sqrt[12]{2^3}$ | 311.1 | |
| Mi | 64 | $\sqrt[12]{2^4}$ | 329.6 | |
| Fa | 65 | $\sqrt[12]{2^5}$ | 349.2 | |
| Fa# o Solb | 66 | $\sqrt[12]{2^6}$ | 370.0 | |
| Sol | 67 | $\sqrt[12]{2^7}$ | 390.0 | |
| Sol# o Lab | 68 | $\sqrt[12]{2^8}$ | 415.3 | |
| La | 69 | $\sqrt[12]{2^9}$ | 440.0 | |
| La# o Sib | 70 | $\sqrt[12]{2^{10}}$ | 466.2 | |
| Si | 71 | $\sqrt[12]{2^{11}}$ | 493.9 | |
| Do | 72 | $2:1$ | 523.3 |
n = [60,72,64,66,58] # MIDI note
for i in n:
PNote(i, 0.5, 127)
Dinamica o ampiezza ¶
Questo parametro in termini musicali è dato dal rapporto tra i suoni più deboli (pianissimissimo) e quelli più forti che caratterizzano la dinamica di un brano.
Intensità sonora ¶
La dinamica di un suono in fisica si definisce con il termine ampiezza in quanto descrive l’ampiezza delle variazioni dell’onda sonora rispetto allo stato di quiete e fornisce una misura dell’energia da essa trasportata.
Se prendiamo in considerazione l'aspetto fisico acustico e non la percezione umana questo parametro è indipendente dalla frequenza e per convenzione rappresentato da valori compresi tra -1.0 e +1.0.
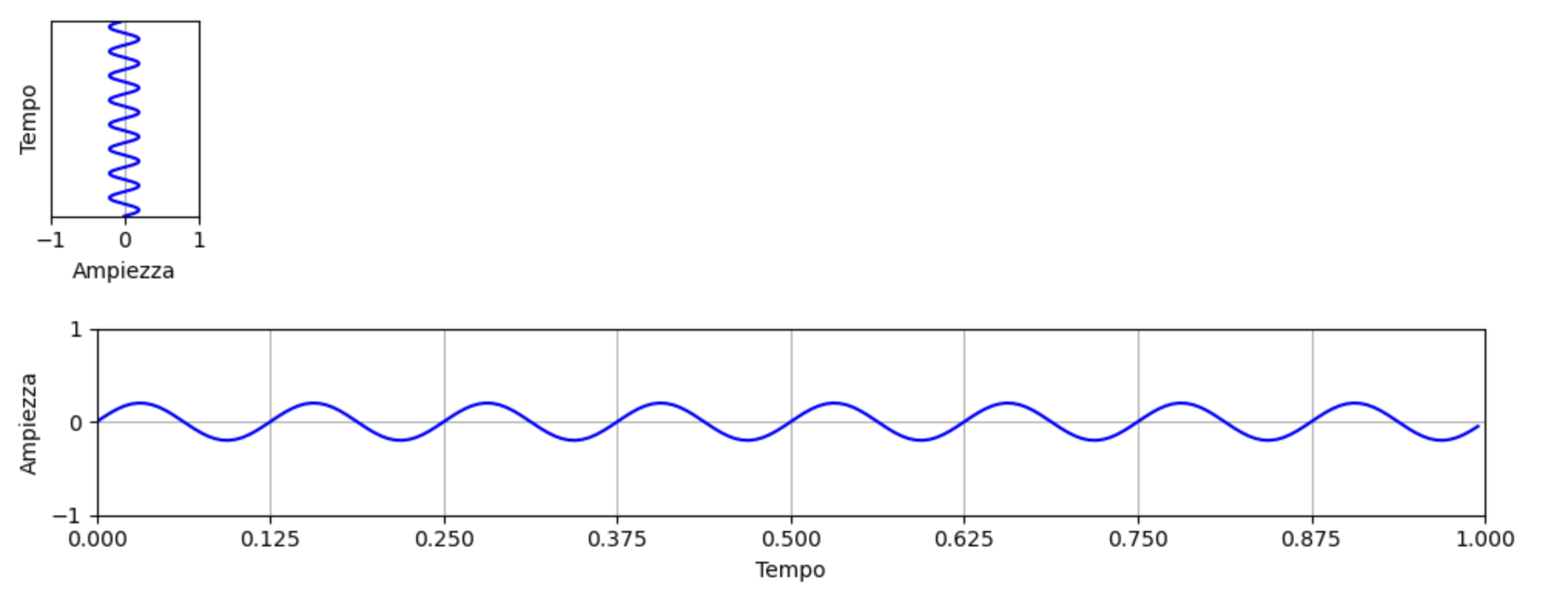
Anche per quanto riguarda la misurazione dell'ampiezza di un suono possiamo farla attraverso unità di misura assolute o relative.
In ambito musicale è importante misurare non solo le ampiezze ma anche i rapporti che intercorrono tra suoni con intensità differenti.
Rappresentazioni ¶
Possiamo specificare questo parametro in due diversi tipi di notazione simbolica:
Simboli musicali - I valori sono quasi sempre relativi al contesto musicale, ovvero un "forte" in una sonata per violino barocca non ha la stessa intensità di un "forte" dato agli ottoni in un poema sinfonico di R.Strauss.
A differenza delle altezze dove esiste una corrispondenza precisa tra la rappresentazione simbolica in notazione musicale e la misurazione fisica, le dinamiche musicali sono caratterizzate da una rilevante soggettività che va ben oltre alla semplice misura fisica delle ampiezze dei suoni.

Valori numerici relativi a diverse unità di misura:
Lineare - Unità di misura assoluta espressa in valori decimali compresi tra 0.0 e 1.0. La più lontana dalla percezione umana riguardo i cambiamenti di intensità dei suoni.
Key Velocity (MIDI) - Unità di misura assoluta espressa in valori interi compresi tra 0 e 127. La meno precisa a causa del limitato numero di livelli dovuto alla disponibilità di soli 7 bit del protocollo MIDI.
Quartica - Unità di misura assoluta espressa in valori decimali compresi tra 0.0 e 1.0. La più vicina alla percezione umana riguardo i cambiamenti di intensità dei suoni. $$a^4$$
Decibels (dB) - Unità di misura relativa espressa in valori decimali compresi tra 0.0 e -inf (o +inf a seconda del tipo di misurazione). Misura la differenza di intensità tra l'ampiezza lineare di un suono rispetto a un'ampiezza di riferimento. $$20*\log_{10}(\frac{a}{a0})$$
Alcuni rapporti tra queste unità di misura.
| Segno | Vel | lin | quart | dB | |
|---|---|---|---|---|---|
| pppp | 12 | 0.1 | 0.0001 | -20 | |
| ppp | 24 | 0.2 | 0.0016 | -14 | |
| pp | 44 | 0.3 | 0.0081 | -10 | |
| p | 54 | 0.4 | 0.0256 | -8 | |
| mp | 64 | 0.5 | 0.0625 | -6 | |
| mf | 74 | 0.6 | 0.1296 | -4 | |
| f | 84 | 0.7 | 0.2401 | -3 | |
| ff | 94 | 0.8 | 0.4096 | -2 | |
| fff | 114 | 0.9 | 0.6561 | -1 | |
| ffff | 127 | 1.0 | 1.0000 | 0 |
a = [20,127,24,100,58,60,127,10,60,120,30] # MIDI velocity
for i in a:
PNote(92, 0.5, i)
Strumenti o timbro¶
Il timbro è quella particolare qualità del suono che permette di distinguere due suoni con uguale ampiezza e altezza e consente all'ascoltatore di identificare la fonte sonora, rendendola distinguibile da ogni altra.
Spettri sonori ¶
Il timbro dei suoni naturali è influenzato da moltissimi parametri come le proprietà fisiche della sorgente sonora e dal modo in cui è messa in vibrazione.
Tutti questi parametri concorrono a formare una rappresentazione fisica del timbro di quel suono ovvero la sua forma d'onda.
Nelle celle sottostanti sono illustrate tre diverse forme d'onda:
- suono puro - è formato da una sola onda sinusoidale con propria frequenza, ampiezza e fase. Non esiste in natura e può solo essere sintetizzato.

- suono complesso periodico - è caratterizzato dalla presenza di più sinusoidi (suoni parziali) sovrapposte, ognuna con una propria frequenza, una propria ampiezza e una propria fase che hanno un qualche tipo di relazione tra loro.

- suono complesso aperiodico (rumore) - come il precedente ma i parametri non sono in relazione tra loro.

Suoni parziali ¶
I suoni presenti in natura sono caratterizzati da forme d'onda differenti tra loro e dunque da suoni complessi.
Un suono complesso è il risultato della sovrapposizione di più suoni puri secondo il teorema enunciato dal fisico francese J.Fourier nei primi anni dell'800:
Qualunque segnale periodico può essere scomposto nella somma di un eventuale termine costante e di segni sinusoidali, dei quali il primo, avente lo stesso periodo e quindi la stessa frequenza del segnale considerato, si chiama prima armonica o fondamentale, e gli altri, aventi periodi sottomultipli e quindi frequenze multiple, si chiamano armoniche superiori
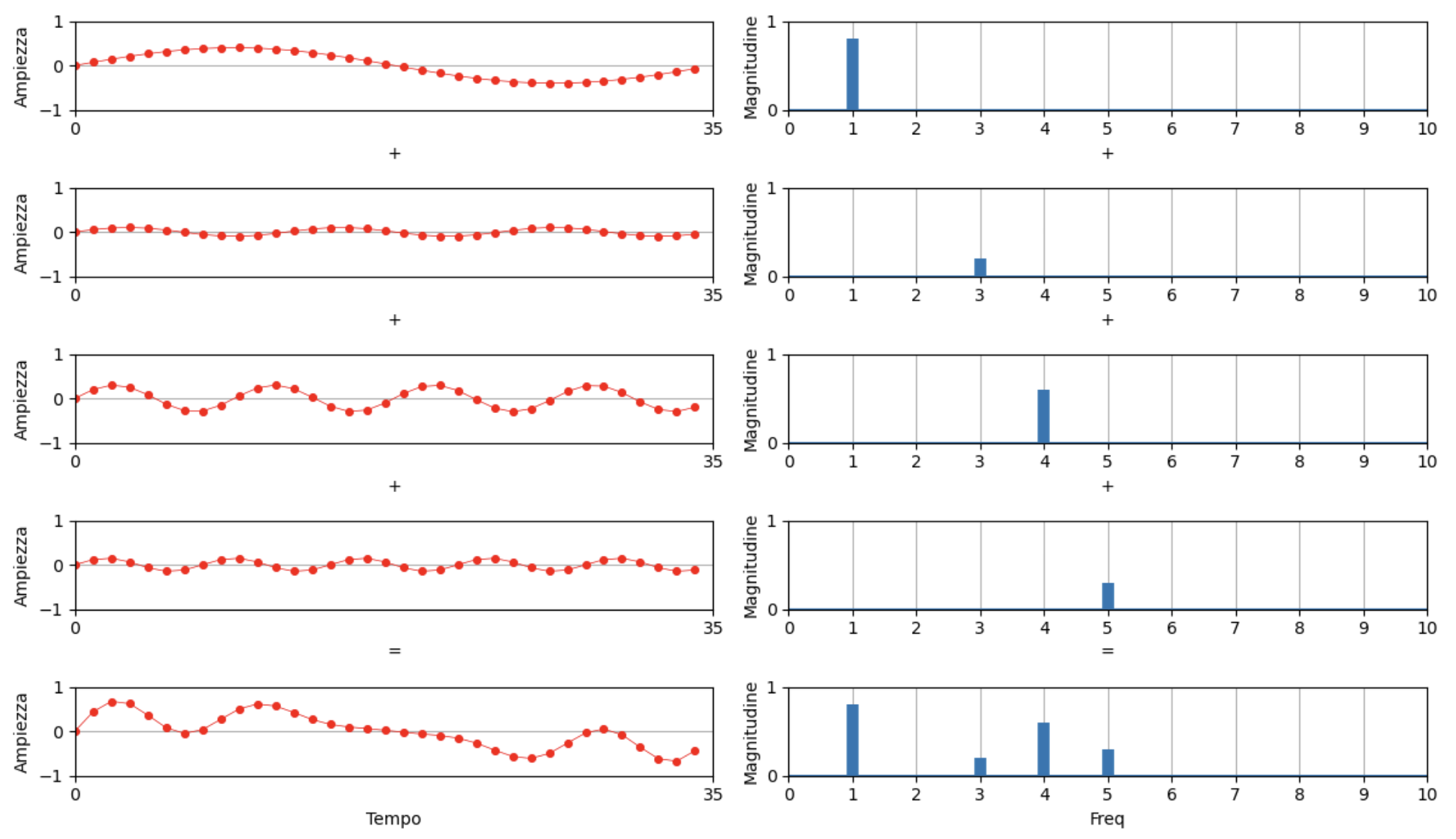
Rappresentazione attraverso simboli musicali:

Ogni suono puro che concorre a formare uno spettro complesso può essere chiamato suono armonico o parziale.
La differenza terminologica tra queste due definizioni è sottile e implica la conoscenza del tipo di spettro a cui si riferisce.
Gli spettri sonori possono essere suddivisi in due grandi famiglie:
Spettri armonici. Le frequenze dei parziali seguono rapporti formati da numeri interi e la cui forma d'onda può essere solamente periodica.:
- 1:1 - Fondamentale
- 1:2 - Primo armonico
- 1:5 - Quarto armonico
- 1:8 - Settimo armonico
- ...
- 1:n - Ennesimo armonico

- Spettri inarmonici. Le frequenze dei parziali non seguono alcun rapporto particolare.

Possiamo affermare che tutti i suoni possibili sono formati da spettri compresi tra:
- suono puro (la singola sinusoide - periodico) e
- suono più complesso (il rumore bianco - aperiodico)
le cui caratteristiche oscillano tra suoni inarmonici, suoni quasi armonici e suoni armonici.

Tempo e pulsazioni¶
La misurazione del tempo è stata la prima scienza esatta dell’antichità.
Le uniche certezze provenivano dai fenomeni astronomici.
I suoni (e di conseguenza la musica) esistono solo nel tempo, in un tempo non reversibile se non nella memoria.
Per questo motivo dobbiamo definire alcuni parametri atti a misurare il tempo, o meglio misurare una sequenza di eventi o azioni che si svolgono nel tempo per poterli organizzare (comporre) in ritmo e tradurli in linguaggi simbolici interpretabili da esecutori umani o da software.
Onsets, delta e durate ¶
Possiamo specificare qualsiasi tipo di evento sonoro nel tempo attraverso combinazioni tra i seguenti parametri:
Onsets - tempi assoluti incrementali a partire da un tempo 0 iniziale.
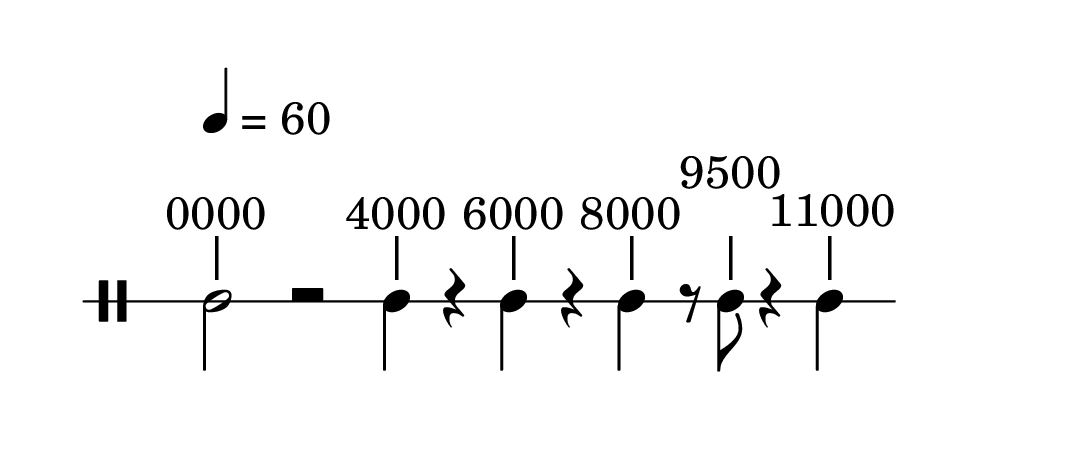
Tempi delta - la misurazione del tempo che intercorre tra due eventi consecutivi.

Durate - la misurazione della durata di uno o più eventi.

A seconda delle situazioni e degli ambienti software possiamo impiegare:
- tempi delta e durate
- onset e durate
In entrmbe i casi se:
- tempo delta = durata - legato
- tempo delta < durata - pause tra gli eventi
- tempo delta > durata - sovrapposizione polifonica

Unità di misura ¶
Possiamo specificare ognuno di questi parametri attraverso due unità di misura differenti.
- Tempo assoluto in secondi o millisecondi - tipica rappresentazione nei linguaggi informatici
onsets = (0.0, 0.25, 0.5, 1) # secondi durate = (0.25, 0.25, 0.5, 2) delta = ( 0.25, 0.25, 0.5 ) onsets = (0.0, 250, 500, 1000) # millisecondi durate = (250, 250, 500, 2000) delta = ( 250, 250, 500 )
Tempo relativo in battiti per minuto o tempo metronomico (bpm) - suddivisioni di una pulsazione regolare (tactus o beat):
Possiamo rappresentare i valori in quattro modi diversi.
Notazione simbolica - sistema di simboli (grafici, alfabetici o altro).
Simboli numerici 16 16 8 2 4 Simboli alfabetici s s e h q Simboli musicali
Notazione frazionale - numero di suddivisioni del beat.
1/4 1/4 1/2 2/1 1/1 (beat = quarto = 1)
Fattore di moltiplicazione dell'unità - valore numerico corrispondente al risultato della notazione frazionale.
0.25 0.25 0.5 2 1 (beat = quarto = 1)
Notazione proporzionale - ratio (proporzione) tra suddivisioni del beat.
1:4 1:4 2:4 8:4 4:4 (quantità : n_suddivisioni_beat)
Suddivisioni e rappresentazioni ¶
Le suddivisioni del tempo musicale sono definite attraverso i simboli illustrati nel seguente schema:
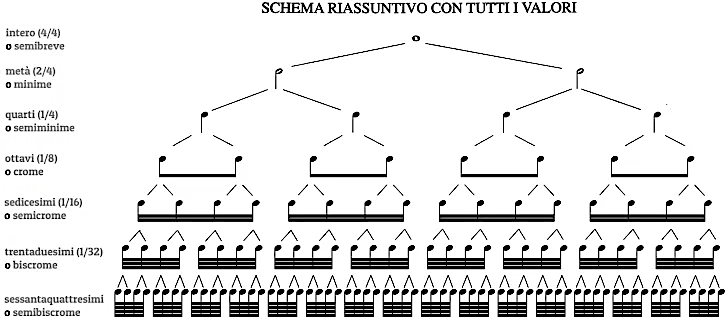
Possono assumere la forma di gruppi regolari dove le suddivisioni sono $1/2^{n}$ come quelle illustrate nello schema precedente


a = [1,4,2,8,2,1] # Suddivisioni
for i in a:
for n in range(i):
PNote(60,1/i,127)
Possono assumere la forma di gruppi irregolari caratterizzati dalle suddivisioni $1/3^{n}$ $1/5^{n}$ $1/7^{n}$ $1/11^{n}$ $1/13^{n}$, etc

a = [3,5,3,7,1,5] # Suddivisioni
for i in a:
for n in range(i):
PNote(60,1/i,127)
Le due categorie si possono ovviamente mescolare in gruppi misti.

a = [1,2,3,2,5,3,4,1] # Suddivisioni
for i in a:
for n in range(i):
PNote(60,1/i,127)
Simboli per le pause:


a = [60, 0, 64, 67, 0, 72, 0, 76] # Pitch 0 = pausa
d = [1 , 1, 0.5, 0.5, 0.5, 1.5, 1, 3]
for i in range(len(a)):
PNote(a[i],d[i],127)
Nel frammento melodico precedente notiamo la presenza di un punto di valore.
Quando è presente raddoppia della metà la durata.

a = [60, 64, 62, 65, 64, 67, 65, 67, 69, 71, 72, 67] # Pitch 0 = pausa
d = [3/4, 1/4, 3/2, 1/2, 7/8, 1/8, 1/8, 1/8, 1/8, 1/8, 3/2, 2]
for i in range(len(a)):
PNote(a[i],d[i],127)
Possiamo allungare la durata di una nota anche attraverso le legature di valore.

Tempi e misure ¶
In matematica dividiamo decine centinaia, migliaia etc. con un punto per renderli più leggibili - $1.000.000$ vs $1000000$.
In informatica vale lo stesso con il concetto di bit e byte (1 byte = 8 bit) o di parola binaria.
In musica i valori di tempo appena enunciati sono inseriti in griglie temporali che possiamo definire timeline per una DAW oppure battute o misure in una partitura.

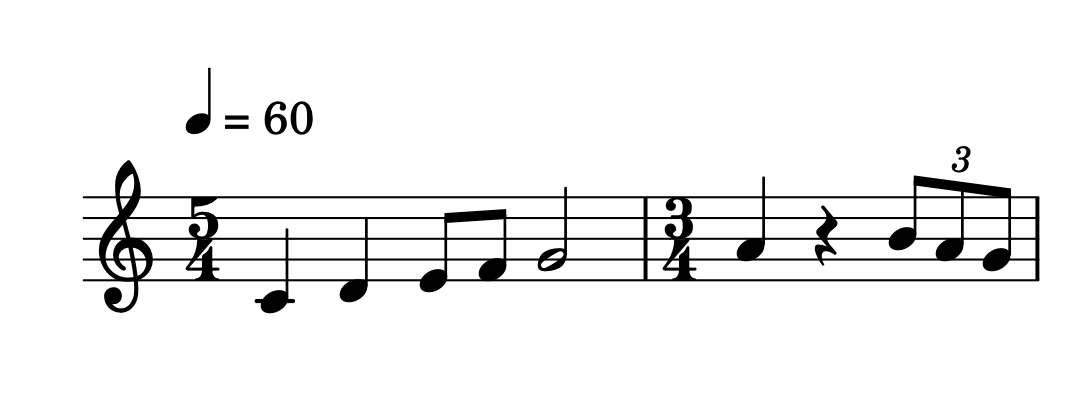
Notiamo l'impiego sia di tempi assoluti che di tempi relativi.
La notazione si avvale di indicazioni di tempo sotto forma di frazione (3/4, 4/4, 6/8, et.) che indicano il numero di unità in una battuta o misura.
Le misure sono separate attraverso linee verticali (barline o stanghette di battuta).
I tempi (indicazioni di tempo) possono essere semplici:
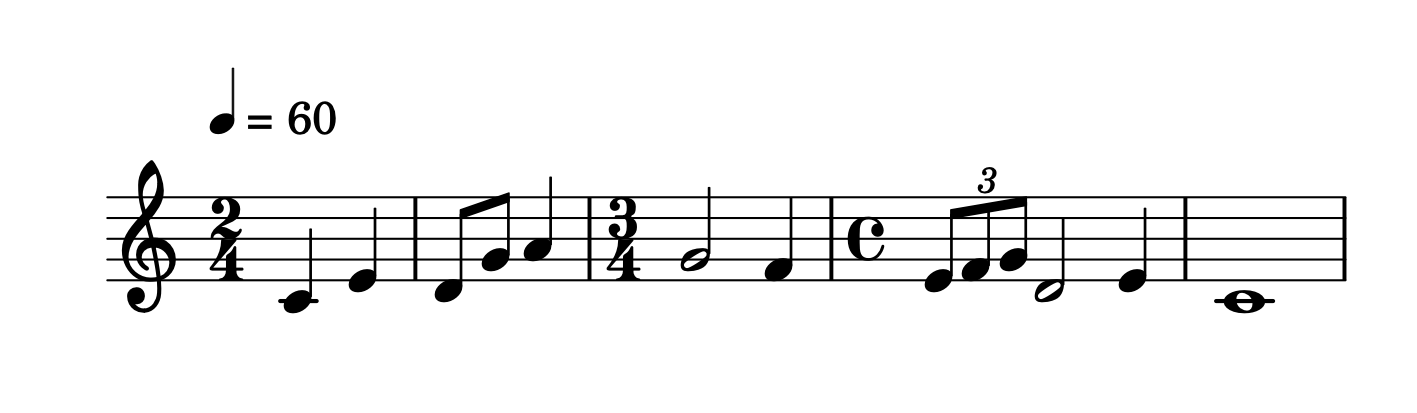
a = [60, 64, 62, 67, 69, 67, 65, 64, 65, 67, 62, 64, 60]
d = [1 , 1, 0.5, 0.5, 1, 2, 1, 1/3, 1/3, 1/3, 2, 1, 4]
for i in range(len(a)):
PNote(a[i],d[i],127)
Oppure composti.

a = [60, 64, 62, 67, 69, 67, 65, 64, 65, 67, 62, 64, 60, 67]
d = [2/3, 1/3, 1/3, 1/3, 1/3, 2/3, 1/3, 1/3, 1/3, 1/3, 1/2, 1/2, 1, 1]
for i in range(len(a)):
PNote(a[i],d[i],127)
Terminologia ¶
- Suono - un fenomeno fisico
- Onda sonora - energia meccanica che si propaga nello spazio e nel tempo.
- Sorgente sonora - corpo elastico che produce un suono
- Ricevente - Orecchio o microfono.
- Onde periodiche - fenomeno oscillatorio che si ripete uguale nel tempo.
- Parametri del suono
- altezza o frequenza - sensazione di gravità o acutezza.
- dinamica o ampiezza - sensazione di intensità sonora.
- strumenti timbro - caratteristiche morfologiche di un suono.
- spettro sonoro - definisce il timbro nel dominio delle frequenze.
- suoni parziali o armonici - elementi di uno spettro sonoro.
- forma d'onda - definisce il timbro nel dominio del tempo.
- Rappresentazioni simboliche musicali
- pentagramma - righi musicali che definiscono una voce.
- chiavi - definiscono un'altezza di riferimento sul pentagramma.
- alterazioni - diesis, bemolli, doppi diesis e doppibemolli.
- tagli addizionali - usati per le altezze fuori dal pentagramma.
- Onset - punto nel tempo dove comincia un evento sonoro riferito a un tempo 0.
- Tempo assoluto - misurazione in secondi o millisecondi.
- Tempo relativo - misurazione in beat.
- BPM o MM- tempo metronomico (beat per minuto).
- Gruppi ritmici regolari - suddivisioni del beat per $1/2^n$.
- Gruppi ritmici irregolari - le altre suddivisioni del beat terzina, quintina, etc.
- Punto di valore - raddoppia la durata della metà.
- Legatura di valore - unisce due o più durate.
- Misura o battuta - contenitore di beat.
- Tempi semplici - 2/4, 3/4, 4/4 etc.
- Tempi composti - 6/8, 9/8, 12/8 etc.
Domande sospese ¶
I simboli impiegati nella notazione musicale sono prima scritti (an-notati) da un compositore e successivamente letti e interpretati da un esecutore.
Se esistono, quali sono le informazioni musicali (parametri) che non possono essere scritte in una partitura?
Come puó un interprete ricostruire ció che non é notato?
E' sufficiente che l'interprete e-segua fedelmente la partitura per trasmettere il pensiero musicale originale del compositore?
Dei seguenti frammenti musicali:
- che tipologia di pulsazioni li caratterizza.
- descrivi il tipo di tempo di ognuno e rifletti su come lo descrivi.
- che tipo di rapporti ci sono tra i diversi parametri del suono in ogni brano.
- si percepiscono le differenze tra i tipi di pianoforte impiegato e se sí perché?