Intervalli¶
import os
import sys
path = os.path.abspath('rappresenta')
sys.path.append(path)
from main import *
Definizione¶
Nei capitoli precedenti abbiamo definito attraverso diversi simboli e unità di misura le altezze musicali.
Abbiamo illustrato alcune regole attraverso le quali sono state definite e orgaizzate nel corso dei secoli.
Questi sistemi che abbaimo chiamato scale o temperamenti si basano sul concetto di intervallo.
Un intervallo è definito dal rapporto (o distanza) tra due altezze ed è fondamento di quasi tutti i sistemi (linguaggi) musicali codificati.
Limitiamoci alla loro definizione nel sistema musicale occidentale moderno che si basa sulla scala cromatic temperata.
Per facilitare la comprensione gli esempi in notazione musicale hanno come root pitch il DO ma gli intervalli possono essere definiti a partire da qualsiasi tono.
Intervalli semplici¶
Un intervallo può essere definito in due modi:
Cromatico - ovvero la distanza in semitoni cromatici a partire dal numero 0.

cro = [[0,1], [0,2], [0,3], [0,4], [0,5], [0,6], [0,7], [0,8], [0,9], [0,10], [0,11], [0,12]] # Intervalli cromatici
for i in cro:
for b in i:
n = 60 + b
PNote(n, 0.5, 127)
time.sleep(0.7)
Diatonico - definito da una combinazione di due elementi:
- distanza diatonica - il numero di toni diatonici (gradi o nomi) tra le due altezze (unisono, seconda, terza, quarta, quinta, sesta, settima, ottava,...)

- qualità - di cinque tipi:
- Maggiore (M)
- Minore (m)
- Dimunuita (d)
- Aumentata (A)
- Perfetta (P) o Giusta
Non tutti gli intervalli possiedono le stesse qualità:
Perfetto (P): $\ \ \ \ 1^a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 4^a\ \ \ \ \ 5^a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 8^a$
Maggiore (M): $\ \ \ \ \ \ \ \ \ \ 2^a\ \ \ \ 3^a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 6^a\ \ \ \ \ \ \ 7^a$
Cromatico: $\ \ \ \ \ \ 0\ \ 1\ \ 2\ \ 3\ \ 4\ \ 5\ \ 6\ \ 7\ \ 8\ \ 9\ \ 10\ \ 11\ \ 12\ $
Notiamo come le distanze cromatiche siano 0 2 4 5 7 9 11 ovvero quelle corrispondenti alla moderna scala maggiore.
Notiamo inoltre come gli intervalli perfetti o giusti siano quelli considerati consonanti fin dai tempi di Pitagora.
Minore (m): un semitono meno del maggiore.
Diminuito (d): due semitoni meno del maggiore o un semitono meno del perfetto.
Aumentato (A): un semitono in più sia del maggiore che del perfetto.
dia = [[0,2], [0,4], [0,5], [0,7], [0,9], [0,11], [0,12]] # Intervalli diatonici
for i in dia:
for b in i:
n = 60 + b
PNote(n, 0.5, 127)
time.sleep(0.7)

Gli intervalli diatonici all'interno di un'ottava si chiamano intervalli semplici.
Due Possibili rappresentazioni simboliche:
- Q:d - come ad esempio P:5 = quinta perfetta, dove Q è la qualità e d la distanza diatonica partendo da 1 = unisono.
- $(d, c)$ - come ad esempio (4, 7) = quinta perfetta dove $d$ è la distanza diatonica e $c$ quella cromatica in entrambi i casi partendo da 0 = unisono.
La seguente tabella illustra tutti i 28 possibili intervalli nell'ambito di un ottava.
| Intervallo | Diatonico | Cromatico | Intervallo | Diatonico | Cromatico |
|---|---|---|---|---|---|
| d:0 | 1 | -1 | d:5 | 5 | 6 |
| P:1 | 1 | 0 | P:5 | 5 | 7 |
| A:1 | 1 | 1 | A:5 | 5 | 8 |
| d:2 | 2 | 0 | d:6 | 6 | 7 |
| m:2 | 2 | 1 | m:6 | 6 | 8 |
| M:2 | 2 | 2 | M:6 | 6 | 9 |
| A:2 | 2 | 3 | A:6 | 6 | 10 |
| d:3 | 3 | 2 | d:7 | 7 | 9 |
| m:3 | 3 | 3 | m:7 | 7 | 10 |
| M:3 | 3 | 4 | M:7 | 7 | 11 |
| A:3 | 3 | 5 | A:7 | 7 | 12 |
| d:4 | 4 | 4 | d:8 | 8 | 11 |
| P:4 | 4 | 5 | P:8 | 8 | 12 |
| A:4 | 4 | 6 | A:8 | 8 | 13 |
Notiamo due intervalli che escono dall'ambito dell'ottava: d:0 ovvero l'unisono diminuito e A:8 ovvero lìottava aumentata che sono argomento controverso nei dibattiti sulla teoria della musica.
Intervalli composti¶
Quando gli intervalli superano l'ottava si chiamano composti.
Le distanze diatoniche di ottava sono: 8 15 22 etc. e possiamo trovarle come indicazione di chiave.
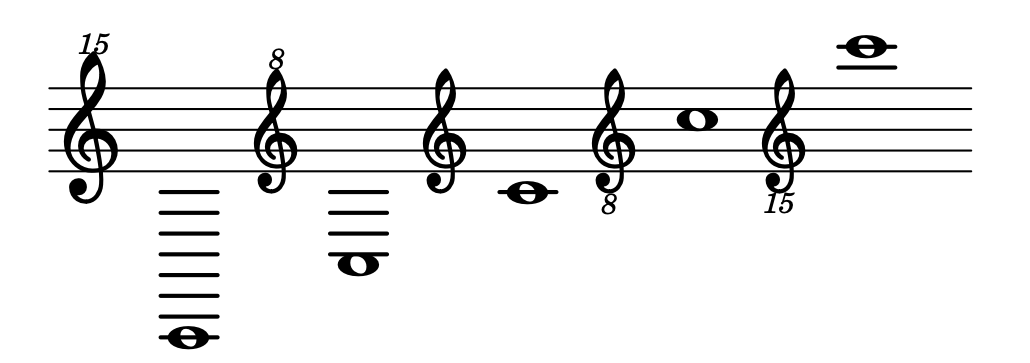
Gli intervalli composti possono essere ridotti ovvero riportati all'interno dell'ottava.

In generale gli intervalli composti suonano più aperti mentre quelli semplici chiusi.
sem = np.array([[0,16], [-2,17]]) # Intervalli composti
com = np.array([[0, 4], [-2, 5]]) # Intervalli ridotti
seq = [sem, com]
for i in seq:
for b in i:
n = 60 + b
PNote(n, 0.5, 127)
time.sleep(0.7)
Questa differenza influisce molto anche sulla condotta delle parti nel contrappunto e nelle disposizioni accordali in armonia dove come vedremo gli accordi possono essere presentati a parti strette:
oppure a parti late:
Operazioni sugli intervalli¶
Operazioni sugli intervalli che sono comuni alle sintassi di diversi linguaggi musicali appartenenti a epoche differenti come contrappunto e dodecafonia.
Pensando queste operazioni in termini matematici e/o informatici dobbiamo tenere presente la differenza semiotica e sintattica tra diatonismo e cromatismo.
Riduzione¶
Un intervallo composto può essere scomposto in due o più intervalli semplici $\rightarrow$ P:12 = P:8 + P5

Il calcolo della riduzione è semplice se si conosce il numero di ottave di distanza che è determinato dalla distanza diatonica.
- Calcoliamo il numero di ottave attraverso la seguente formula che mappa le distanze diatoniche in blocchi di sette (i gradi diatonici in un ottava) partendo da zero.
d = 12 # Intervallo diatonico
if d == 0:
d = 0
else:
d = int(((abs(d)-1)/7) * np.sign(d))
print(d)
1
- Rimuoviamo l'offset di ottave e riduciamo l'intervallo sia diatonicamente che cromaticamente.
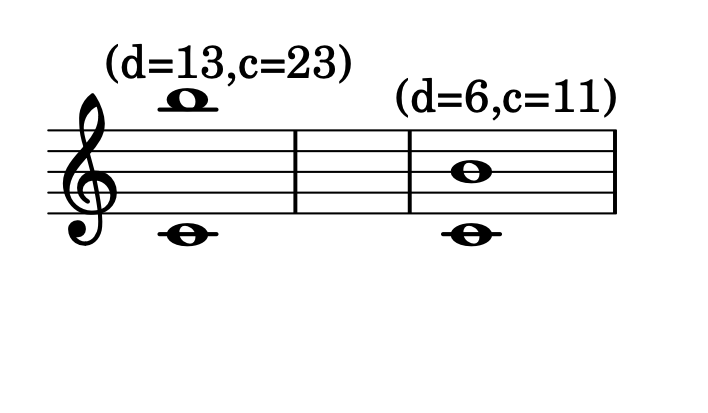
d, c = 13, 23 # distanza diatonica, distanza cromatica partendo da 0 ( Do-Si)
def rid(d=0,c=0):
if d == 0: # prima calcola l'offset di ottave
oct = 0
else:
oct = int(((abs(d)-1)/7) * np.sign(d))
d = d - 7 * oct # dopo riduce
c = c - 12 * oct
return (d,c)
PNote(60, 0.5, 127) # originale
PNote(60 + c, 0.5, 127)
PNote(60, 0.5, 127) # ridotto
PNote(60 + i[1], 0.5, 127)
i = rid(d, c)
print((d, c))
print(i)
(13, 23) (6, 11)
Un la riduzione è un processo ampiamente utilizzato nella musica dodecafonica.

Inversione¶
Per l'inversione diventa importante la differenza tra:
- inversione cromatica - neutra
- inversione diatonica - propria dei linguaggi tonali e contrappuntistici.
Inversione cromatica
Sotto un punto di vista concettuale, matematico e informatico è la più semplice.
Può essere sia positiva che negativa.
Prendiamo un intervallo perno come riferimento assegnando il valore $0$ e:
- se l'intervallo cromatico (semitoni) è positivo lo moltiplichiamo per $-1$.
- se l'intervallo cromatico (semitoni) è negativo lo moltiplichiamo per $1$.
$$Inv(I) = I * -1 = (0, -4)$$
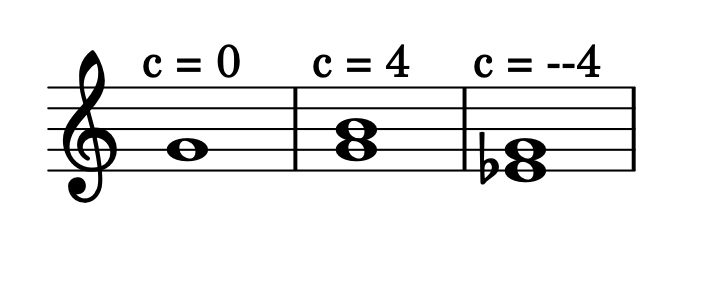
L'inversione cromatica è una delle regole fondamentali del sistema dodecafonico.

Inversione diatonica
L'intervallo diatonico è il rapporto tra due altezze una delle quali è presa come riferimento che in questo caso è la più bassa (l'intervallo è per definizione positivo).
L'inversione avviene semplicemente invertendo questo rapporto trasportando la nota più bassa all'ottava sopra.

Il concetto di inversione diatonica nella tradizione musicale occidentale è importante per diverse ragioni:
- è alla base del concetto di rivolto che incontreremo quando parleremo di accordi in ambito tonale.
- può essere un metodo per ricavare lo stato fondamentale di un'accordo.
La regola per calcolare l'inversione:
Dato un intervallo $(d, t)$ dove $d$ è è la distanza diatonica e $t$ la qualità ovvero il tipo di intervallo possiamo calcolarne l'inversione attraverso la formula: $$(9 - d, t^{m})$$ dove $t^{m}$ è definito dal seguente mapping:
- M $\rightarrow$ m
- m $\rightarrow$ M
- d $\rightarrow$ A
- A $\rightarrow$ d
- P $\rightarrow$ P
La seguente tabella illustra tutte le inversioni intervallari nell'ambito di un ottava (unisono con indice 1).
| Originale | Inversione | |
|---|---|---|
| unisono | D:1 | A:8 |
| P:1 | P:8 | |
| A:1 | d:8 | |
| d:2 | A:7 | |
| seconda | m:2 | M:7 |
| M:2 | m:7 | |
| A:2 | d:7 | |
| terza | d:3 | A:6 |
| m:3 | M:6 | |
| M:3 | m:6 | |
| A:3 | d:6 | |
| quarta | d:4 | A:5 |
| P:4 | P:5 | |
| A:4 | d:5 | |
| quinta | D:5 | A:4 |
| P:5 | P:4 | |
| A:5 | d:4 | |
| sesta | d:6 | A:3 |
| m:6 | M:3 | |
| M:6 | m:3 | |
| A:6 | d:3 | |
| settima | d:7 | A:2 |
| m:7 | M:2 | |
| M:7 | m:2 | |
| A:7 | d:2 | |
| ottava | d:8 | A:1 |
| P:8 | P:1 | |
| A:8 | d:1 |
Formule
Esaminiamo alcune formule per l'inversione di intervalli sia negativi che positivi.
In questi casi il risultato è sempre ridotto nell'ottava in quanto stiamo parlando di intervalli in senso assoluto (teorico) e non melodico.
Intervalli semplici
$$Inv(I) \equiv Inv((d,c)) \equiv P:8 - I = (7,12) - (d,c) = (7-d, 12-c)$$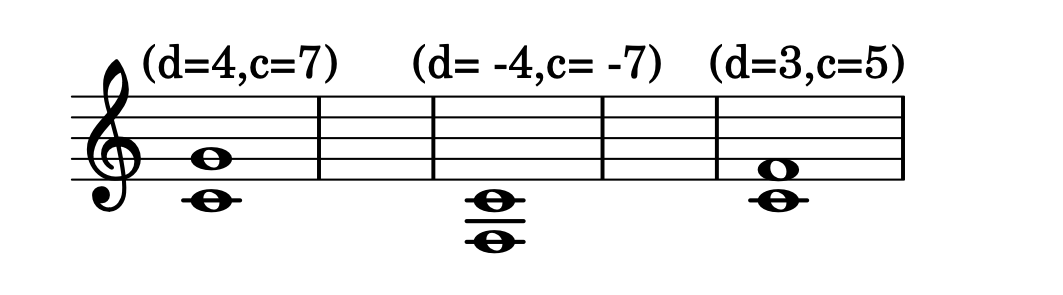
d, c = 4, 7 # distanza diatonica, distanza cromatica partendo da 0 (Do - Sol)
def inv(d=0,c=0):
d = (np.sign(d) * 7) - d
c = (np.sign(d) * 12) - c
return (d,c)
PNote(60, 0.5, 127)
PNote(60 + c, 0.5, 127)
PNote(60, 0.5, 127)
PNote(60 + i[1], 0.5, 127)
i = inv(d, c)
print((d,c))
print(i)
(4, 7) (3, 5)
Intervalli composti
$$Inv(I) \equiv sign(I) * P:8 - Red(I) \equiv \pm1 * (7, 12) - Rid(d, c)$$
d, c = 9, 16 # distanza diatonica, distanza cromatica partendo da 0 (Do - Sol)
r = rid(d,c)
def inv(d=0,c=0):
d = (np.sign(d) * 7) - d
c = (np.sign(c) * 12) - c
return (d,c)
i = inv(r[0], r[1])
PNote(60, 0.5, 127)
PNote(60 + c, 0.5, 127)
PNote(60, 0.5, 127)
PNote(60 + i[1], 0.5, 127)
print((d,c))
print(r)
print(i)
(9, 16) (2, 4) (5, 8)
L'inversione diatonica è una delle regole fondamentali del contrappunto.
Così come dell'armonia tonale.

Somma¶
Possiamo sommare o sottrarre tra loro due intervalli $I = (d,c)$ con $J = (e,f)$
$$I \pm J \equiv (d \pm e,\ c \pm f)$$$$P:5 + M:3 = (4, 7) + (2, 4) = (4 + 2, 7 + 4) = (6, 11) = M:7$$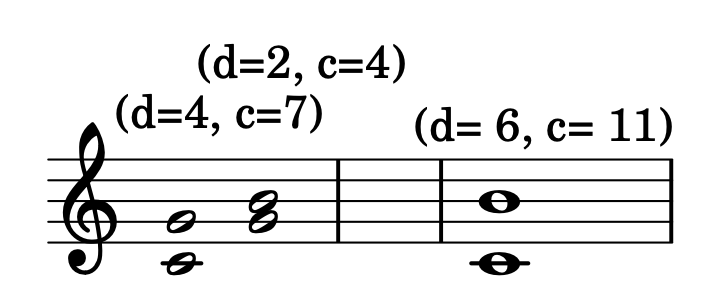
La seguente tabella illustra alcune somme tra intervalli.
| + | P:1 | M:2 | m:3 | M:3 | d:4 | P:4 | P:5 | M:6 | M:7 |
|---|---|---|---|---|---|---|---|---|---|
| P:1 | P:1 | M:2 | m:3 | M:3 | d:4 | P:4 | P:5 | M:6 | M:7 |
| M:2 | M:2 | M:3 | P:4 | A:4 | d:5 | P:5 | M:6 | M:7 | A:8 |
| m:3 | m:3 | P:4 | d:5 | P:5 | d:6 | m:6 | m:7 | P:8 | M:9 |
| M:3 | M:3 | A:4 | P:5 | A:5 | m:6 | M:6 | M:7 | A:8 | A:9 |
| d:4 | d:4 | d:5 | d:6 | m:6 | X | d:7 | d:8 | m:9 | m:10 |
| P:4 | P:4 | P:5 | m:6 | M:6 | d:7 | m:7 | P:8 | M:9 | M:10 |
| P:5 | P:5 | M:6 | m:7 | M:7 | d:8 | P:8 | M:9 | M:10 | A:11 |
| M:6 | M:6 | M:7 | P:8 | A:8 | m:9 | M:9 | M:10 | A:11 | A:12 |
| M:7 | M:7 | A:8 | M:9 | A:9 | m:10 | M:10 | A:11 | A:12 | A:13 |
Notiamo che al centro della tabella c'è una X.
La somma d:4 + d:4 non è valida. $$(3,4)+(3,4) = (6,8)$$
$(6,8)$ non esiste come intervallo.
Compiere operazioni aritmetiche sugli intervalli è dunque un'operazione pratica in quanto matematicamente ha diverse eccezioni.
Anche questa è un'operazione comune a diversi linguaggi musicali e si usa principalmente per trasporre profili melodici o serie dodecafoniche.
Monodia, contrappunto, armonia, serialismo ¶
Il conccetto di intervallo assume diverse funzioni a seconda del sistema sintattico nel quale è ipiegato.
in un brano monodico (anche accompagnato) assume una direzione orizzontale e caratterizza il profilo melodico
in un brano costruito attraverso le regole del contrappunto (punctum contra punctum) pur mantenendo la dimensione orizzonatale è anche alla base delle regole per la condotta e sovrapposizione delle voci.
in un brano costruito attraverso le regole del sistema tonale armonico assumono una dimensione verticale in quanto definiscono i tipi di accordi.
in un brano costruito secondo le regole dodecafoniche o seriali assumono una dimensione neutra.
Terminologia ¶
- Intervallo
- cromatico - distanza in semitoni da 0 (root note).
- diatonico - due elementi:
- distanza diatonica - distanza in toni diatonici.
- qualità (M,m,d,A,P)
- semplice - entro l'ottava
- composto - oltre l'ottava
- positivo - ascendente
- negativo - discendente
- Operazioni sugli intervalli
- riduzione - riportare nell'ottava
- inversione
- cromatica - negativo (* -1)
- diatonica - positivo (ottava alta)
- somma - trasposizioni
Domande sospese¶
La rappresentazione diatonica e quella cromatica non sempre collimano con la percezione sonora
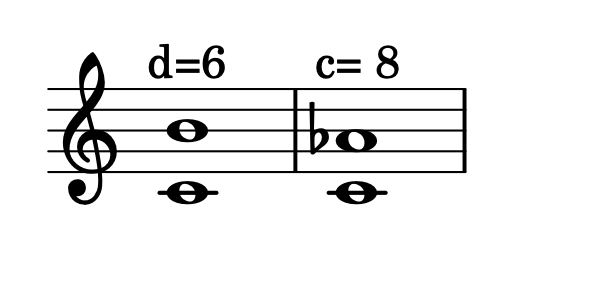
Prendiamo come esempio questi due intervalli:

- entrambi sono una quinta perfetta (o giusta).
- all'ascolto risultano simili.
- la distanza cromatica è identica.
- la distanza diatonica è diversa (enarmonia).
Riflettiamo sui concetti di segno sonoro e segno musicale e sulle loro rappresentazioni e significati.
Possiamo considerare
- la rappresentazione cromatica come neutra senza alcun significato sintattico musicale implicito e dunque più adatta ad essere impiegata per i segni sonori e nel mondo dei linguaggi informatici (linguaggi formali) mentre
- la rappresentazione diatonica assume senso e significato solo all'interno di un linguaggio musicale specifico come quello della tradizione occidentale per cui nel primo caso gli intervalli sono uguali nel secondo sono diversi (il primo è una quinta perfetta mentre il secondo una sesta diminuita).
Questa considerazione è importante anche riguardo alla scelta di strategiae informatiche riguardanti gli intervalli.
- gli intervalli caratterizzano moltissimi aspetti estremamante diversi tra loro che veicolano l'espressività musicale (andamento melodico, tonalità d'impianto, funzioni armoniche, etc.). Esiste qualcosa che li accomuna ovvero un salto di terza maggiore o minore in un profilo melodico (orizzontale) può assumere un significato simile dello stesso intervallo in una relazione armonica?
Rappresentazioni informatiche¶
Per questo argomento l'unico approfondimento informatico è legato al codice.
IntervalType ed Interval
IntervalType è una classe che indicizza i simboli riferiti alle qualità degli intervalli restituendoli sotto forma di stringhe.
- 1 = Major
- 2 = Minor
- 3 = Diminished
- 4 = Augmented
- 5 = Perfect
Servirà come utilità in altre classi
tipo = 2
q = IntervalType(tipo)
print(q)
Minor
Interval invece provvede a tutte le operazioni descritte in questo capitolo.
Si basa su tre proprietà:
- interval_type: la qualità dell'intervallo.
- diatonic_distance: la distanza diatonica dall'origine $1$.
- chromatic_distance: il numero di semitoni sia positivo che negativo dall'origine $0$.
Ci sono diversi modi per creare un intervallo (istanza) illustriamo il più immediato.
i = IntervalN.parse('M:3')
print(i)
M:3
Possiamo recuperare distanza cromatica e distanza diatonica.
d = i.diatonic_distance
c = i.chromatic_distance
print(c)
PNote([60, 60 + c], 1, 127)
4
<main.PNote at 0x126939dc0>
Possiamo calcolare l'inversione negativa
n = i.negation()
print(n)
c = n.chromatic_distance
print(c)
PNote([60, 60 + c], 1, 127)
-M:3 -4
<main.PNote at 0x11f2018e0>
Possiamo calcolare l'inversione (come il precedente ma riportato nell'ottava)
n = i.inversion()
print(n)
c = n.chromatic_distance
print(c)
PNote([60, 60 + c], 1, 127)
m:6 8
<main.PNote at 0x12a97b560>
Possiamo calcolare la riduzione di intervalli composti
ia = IntervalN.parse('M:10')
ic = ia.reduction()
print(ia, ic)
ca = ia.chromatic_distance
cc = ic.chromatic_distance
PNote([60, 60 + ca], 1, 127)
PNote([60, 60 + cc], 1, 127)
M:10 M:3
<main.PNote at 0x12afd5c10>
Possiamo sommare o sottrarre intervalli attraverso operazioni di overloadin ( ___add___, etc. ) correggendo le somme impossibili attraverso un mapping interno.
ia = IntervalN.parse('P:5')
ib = IntervalN.parse('M:3')
ic = ia + ib
print(ia, ib,ic)
PNote([60, 60 + ia.chromatic_distance], 1, 127)
PNote([60, 60 + ib.chromatic_distance], 1, 127)
PNote([60, 60 + ic.chromatic_distance], 1, 127)
P:5 M:3 M:7
<main.PNote at 0x105ff3fe0>
sottrai = ia - ib
print(sottrai)
PNote([60, 60 + sottrai.chromatic_distance], 1, 127)
m:3
<main.PNote at 0x12bb9a600>
ia += ic
print(ia)
A:11
ia -= ic
print(ia)
P:5
Possiamo ottenere l'inizio e la fine sotto forma di altezza definita specificandola con DiatonicPitch.
i = IntervalN.parse('P:5')
s = i.get_start_pitch(DiatonicPitch.parse('C:3'))
e = i.get_end_pitch(DiatonicPitch.parse('F:2')) # Prova...
print(s, e)
F:2 C:3
Possiamo notare come la classe DiatonicPitch che sembrava inutile ci serve in questo contesto per definire un altezza assoluta dalla quale calcolare un intervallo.