Home

Percezione, dinamica e agogica

• Introduzione
  • Frequenze e intervalli
  • Intensità sonora
  • Tempo e pulsazioni
• Dinamiche e Tempi variabili
• Terminologia
• Domande sospese
• Rappresentazioni informatiche
  • Codice
  • Musica
  • Suono

import os
import sys

path = os.path.abspath('rappresenta')
sys.path.append(path)                     
from main import *      

Introduzione

Nei capitoli precedenti abbiamo assoldato che:

• il suono è un fenomeno fisico misurabile attraverso strumenti di precisione (fonometri) i cui parametri sono definiti dalla fisica acustica.
  • quali sono i parametri oggetttivamente misurabili delle onde sonore?
  • quali sono le leggi fisiche che li governano?

• la percezione del suono è invece una valutazione soggettiva e gli effetti che esso produce sull'essere umano sono studiati e descritti dalla psicoacustica.
  • quali sono i parametri soggettivi che ci permettono di comprendere un suono?
  • quali sono i processi attraverso i quali definiamo le sue caratteristiche soggettive?

Cercando di collegare tra loro i due aspetti possiamo domandarci quali sono le caratteristiche oggettive dell’apparato di ricezione (orecchio) ed elaborazione (cervello) che danno luogo alle caratteristiche percepite a partire dai paramtri fisici oggettivi dell’onda sonora?

Una possibile risposta è data dall'intersecarsi di diversi fenomeni posti su piani distinti:

1. fisico - vibrazione dell`oggetto sorgente e propagazione dell’onda sonora.
2. fisico-fisiologico - interazione tra onda sonora e orecchio.
3. fisiologico - trasduzione del segnale ad opera del sistema percettivo.
4. fisiologico-psicologico - riconoscimento e cognizione del segnale nonchè dei suoi correlati emotivi.
5. cognitivo-linguistico - interpretazione e attribuzione di un significato ai suoni.
6. linguistico-formale - riconoscimento della struttura linguistica o musicale dei suoni.
7. antropologico-culturale - sviluppo di particolari forme e linguaggi verbali o musicali nelle diverse culture e società umane.

Alcuni di questi piani li abbiamo già esplorati in modo più o meno approfondito.

A compendio di questo percorso osserviamo il piano 3 riguardo tre parametri fondamentali:

• Altezze e intervalli.
• Intensità e dinamica.
• Tempo o ritmo.

Frequenze e intervalli

Per quanto riguarda questo parametro sappiamo che:

• le scale musicali osservate nel capitolo dedicato sono realizzate attraverso suddivisioni aritmetiche dell'intervallo di ottava. Nello specifico la scala cromatica segue una progressione aritmetica (sequenza di numeri con una differenza costante tra i numeri.
• i suoni armonici e l'intervallo di ottava seguono invece una progressione geometrica (sequenza di numeri con un rapporto costante).

Il piano antropologico-linguistico-formale è derivato dal precedente ma si basa su differenze tra altezze (intervalli - lineare).

Il piano fisiologico-percettivo si basa su rapporti tra altezze (ratio - logaritmico).

Questo vale per suoni puri, timbri complessi complicano le cose.

Intensità sonora

L'ampiezza di un suono o di un segnale audio è compresa per definizione tra -1 e 1 ed è un valore assoluto.

L`intensità sonora (o volume) di un suono è anch'essa misurabile e l'unità di misura è $W/m^2$.

Nel caso di suoni puri è proporzionale al quadrato dell'ampiezza di picco.

Così come le frequenze udibili sono comprese tra 20 e 20.000 Hz le intensità sono comprese tra:

• Soglia dell'udito - la minima intensità sonora $I_{\mathrm {min} }$ percepibile dall'orecchio umano. Sebbene anch'essa varia da una persona all'altra è definibile per un suono puro a 1.000Hz (suono di riferimento per quasi tutte le principali misurazioni acustiche e psicoacustiche) come $I_{\mathrm {min}} = 10^{-12}W/m^2$ ovvero una variazione della pressiione atmosferica di soli $20 {\mu }Pa$.

• Soglia del dolore - la massima intensità sonora oltre la quale il suono viene percepito come una sensazione di dolore $I_{\mathrm {max}} = 1W/m^2$ che è mille miliardi di volte ovvero $10^{12}$ più forte della soglia di udibilità.

Il livello di intensità sonora si misura: $$I({\rm dB_{SIL}})=10 \log_{10} \left(\frac{I}{I_{\rm min}}\right)$$ dove $I_{\rm min}= 10^{-12}{\rm W/m^2}$$

La misurazione in decibel ha diversi vantaggi:

• Il valore relativo alla soglia di udibilità è di 0 dB: $$I_{\rm min}^{\rm (dB)}=10 \log_{10}\left(\frac{I_{\rm min}}{I_{\rm min}}\right)=10 \cdot \log_{10}1=0\ {\rm dB}$$

• il range dinamico è molto esteso (calcoliamo la soglia del dolore): $$I_{\rm max}^{\rm (dB)}=10 \log_{10}\left( \frac{10^{12}I_{\rm min}}{I_{\rm min}}\right)=10\cdot \log_{10}10^{12}=120\ {\rm dB}$$

• l'orecchio umano risponde percettivamente ai cambiamenti di intensità secondo una scala logaritmica ovvero raddoppiando l'ampiezza di un suono non lo percepiamo come il doppio più forte.

  • doppio più forte
  • dieci volte più forte

  Questa maggiore sensibilità più vicina alla percezione umana si ottiene attraverso il fattore di moltiplicazione 10 e che trasforma il Bel in deciBel che rappresenta la differenza minima di intensità tra due suoni che l'orecchio umano può percepire (JSD - Just Noticeable Difference).

L'intensità sonora appena descritta misura in modo assoluto il flusso di energia trasportato dall'onda sonora.

L'intensità sonora percepita (loudness) invece mette in relazione l'ampiezza con altri parametri come frequenza e timbro.

Ascoltiamo il seguente sweep.

Al netto delle risonanze acustiche sentiamo dei crescendo e diminuendo che se osserviamo l'oscillogramma non sono presenti.

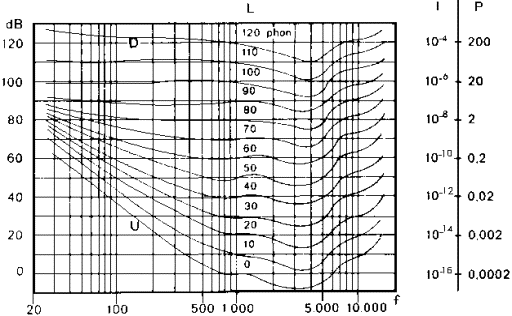
Questo perchè intensità e frequenza non sono parametri indipendenti ma legati tra loro nella percezione umana e seguono un andamento descritto dalle curve isofoniche (diagramma di Fletcher e Munson).

Tempo e pulsazioni

Anche per quanto riguarda i cambiamenti di tempo come accelerando e ritardando la percezione non funziona in modo linerare.

• lineare

• esponenziale

L'accelerando esponenziale ci risulta più naturale e pronunciato di quello lineare.

Dinamiche e tempi variabili

Gli ultimi elementi fondamentali comuni a tutti i linguaggi musicali riguardano il modo in cui le dinamiche e il tempo possono variare nel corso di un brano.

Entrambi i parametri hanno le stesse caratteristiche.

• crescendo e diminuendo.
• accelerando e ritardando.

In entrambi i casi possiamo generalizzare attraverso il concetto di interpolazione ovvero:

• vai dal valore a al valore b in n passi

In musica il numero di passi è sostituito dal tempo e línterpolazione viene chiamata rampa:

• vai dal valore a al valore b in tot tempo

Durante una performance musicale in un crescendo o diminuendo così come in un accellerando e un ritardando:

• i valori di inizio e fine,
• il modo di passare da uno all'altro

sono scelti dall'interprete in base al contesto musicale del brano.

Questi comportamenti possono però essere analizzati attraverso funzioni.

Ci sono principalmente quattro modelli di funzione impiegati in ambito musicale:

• Step - (stepwise) a gradini, le dinamiche o il tempo cambiano in modo discreto e repentino.

  

import matplotlib.pyplot as plt

a = np.ones(5)*0.3
b = np.ones(15)*0.1
c = np.ones(10)*1
d = np.ones(20)*0.6

e = np.concatenate((a,b,c,d))
plt.plot(e, '.')
plt.show()

• Costante - il parametro viene impostato senza modificarlo fino alla fine del brano.

a = np.ones(50)*0.7

plt.plot(a, '.')
plt.show()

• Lineare - (piecewise) il cambiamento avviene in modo costante. Viene percepito come musicalmente debole.

a = np.linspace(0, 1, 50)

plt.plot(a, '.')
plt.show()

• Curvo - (logaritmico o esponenziale) il cambiamento non avviene in modo costante. E' quello che un buon musicista realizza istintivamente in quanto vicino all percezione umana dei cambiamenti.

a = np.linspace(0, 1, 50)**4

plt.plot(a, '.')
plt.show()

Quasi sempre all'interno di un brano si susseguono in multisegmenti sia per quanto riguarda il tempo che le dinamiche.

a = np.linspace(0, 0.6, 10)
b = np.ones(5)*0.6
c = np.linspace(0.6, 0.1, 20)
d = np.ones(5)*0.1
e = np.ones(15)*0.9
f = np.ones(7)*0.5
g = np.linspace(0.85, 1, 25)**4
h = np.linspace(1, 0, 35)**2

e = np.concatenate((a,b,c,d,e,f,g,h))
plt.plot(e, '.')
plt.show()

Terminologia

• Percezione sonora - capacità di ricevere e interpretare soggettivamente le informazioni che raggiungono le orecchie sotto forma di onda sonora.
• Interpolazione - calcolo mediante il quale si determinano valori di una funzione all'interno di un intervallo nel quale ne sono noti solo alcuni.
  • Lineare - il delta tra i valori è costante.
  • Logaritmica o esponenziale - il delta tra i valori non è costante.
• Intensità sonora - grandezza fisica definita come il rapporto tra la potenza di un'onda sonora e l'area della superficie che da essa viene attraversata.
• Soglia dell'usdito - variazione di pressione atmosferica minima per la percezione di un'onda sonora ($20 {\mu }Pa$).
• Soglia del dolore - variazione di pressione atmosferica oltre la quale un'onda sonora viene percepita come sensazione di dolore.
• Range dinamico - il rapporto tra il suono più flebile e quello più forte all'ínterno di un contesto sonoro definito.
• JSD - Just Noticeable Difference - la differenza minima di intensità percepibile dall'orecchio umano (1 decibel).
• Loudness - percezione soggettiva della pressione sonora dipendente dalle relazioni tra ampiezza, frequenza e timbro.
• Sweep - glissato di un suono puro tra 20 e 20.000 Hz ad ampiezza costante.
• Curve isofoniche - diagramma che descrive le relazioni percettive tra intensità sonora e frequenza.
• Crescendo e diminuendo - variazioni dinamiche nel tempo dell'intensità sonora.
• Accelerando e Ritardando - variazioni dinamiche nel tempo delle pulsazioni (beat o tactus).

Domande sospese

• Che tipo di funzione o scopo musicale ha un crescendo o un diminuendo?.
• Che differenza percettiva e musicale c'è tra un crescendo o un diminuemdo di breve durata e uno a livello formale come il crescendo Rossiniano?
• Che funzione semantico musicale hanno le messe di voce di epoca barocca?
• Che tipo di evoluzione hanno avuto le variazioni dinamiche nella storia della musica occidentale?
• Che tipo di relazioni hanno avuto con l'espressività presente in altri ambiti artistici di una stessa epoca e/o estetica culturale.
• Descrivere i diversi tipi di variazioni dinamiche, relazioni intervallari e variazioni temporali del brano seguente (c'è tutto ciò di cui abbiamo parlato).

• Che tipo di differenza intercorre tra un accelerando e/o ritardando misurato e uno che segue un qualche tipo di curva?

Rappresentazioni informatiche

Codice

Nel modulo python che stiamo impiegando per la rappresentazione informatica le funzioni descritte nel paragrafo precedente sono definite in classi dedicate.

• StepwiseFunction([(x, y), (x,y), (x,y)...]) - sequenza di più punti senza interpolazione definiti attraverso coordinate cartesiane.

punti = [(1,1),(4,3),(6,11),(9,8)]
f     = StepwiseFunction(punti)

out = []
for i in range(14):
    out.append(f.eval(i))
print(out)

[1, 1, 1, 1, 3, 3, 11, 11, 11, 8, 8, 8, 8, 8]

• PiecewiseLinearFunction([(x, y), (x,y), (x,y)...]) - interpolazione lineare tra più punti definiti attraverso coordinate cartesiane.

punti = [(0,1),(9,10)]
f     = PiecewiseLinearFunction(punti)

out = []
for i in range(10):
    out.append(f.eval(i))
print(out)

[1, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10]

• GenericFunction(f, start, end) - sequenza di due punti con interpolazione non lineare.

def quart(x):                                # Funzione quartica
    return x**4
    
f = GenericUnivariateFunction(quart, 0, 0.5) # Funzione, inizio, fine

out = []
for i in range(10):
    out.append(round(f.eval(i*0.1),4))
print(out)

[0.0, 0.0001, 0.0016, 0.0081, 0.0256, 0.0625, 0.1296, 0.2401, 0.4096, 0.6561]

Le possiamo integrare in due classi dedicate alla variazioni di tempo e dinamica.

Per il tempo i valori devono essere indicati in bpm:

• Tempo per definire i cambiamenti di tempo repentini.
• TempoFunction per quelli che si svolgono attraverso qualche tipo di interpolazione. Gli argomenti sono:
  • la funzione da impiegare.
  • la posizione di inizio dell'accelerando o ritardando.

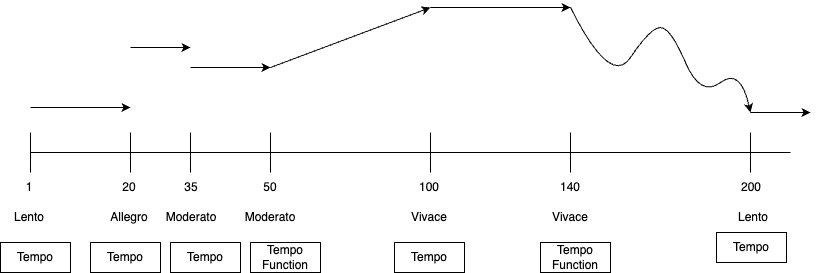
partitura = Score()

partitura.tempo_sequence.add(TempoEvent(Tempo(48,  Duration(1, 4)), Position(0, 1)))    # Lento
partitura.tempo_sequence.add(TempoEvent(Tempo(120, Duration(1, 4)), Position(20, 1)))   # Allegro
partitura.tempo_sequence.add(TempoEvent(Tempo(92,  Duration(1, 4)), Position(35, 1)))   # Moderato

accel = [(Position(50,1), 92), (Position(100, 1),200)]                                  # Accelerando
f = PiecewiseLinearFunction(accel)
partitura.tempo_sequence.add(TempoFunctionEvent(f, Position(50,1)))                     # Moderato --> Vivace
  
partitura.tempo_sequence.add(TempoEvent(Tempo(200,  Duration(1, 4)), Position(100, 1))) # Vivace

rall = [(Position(140,1), 200), (Position(200, 1),48)]                                  # Rallentato in 160 interi
f = PiecewiseLinearFunction(rall)
partitura.tempo_sequence.add(TempoFunctionEvent(f, Position(140,1)))                    # Vivace --> Lento
partitura.tempo_sequence.add(TempoEvent(Tempo(48,  Duration(1, 4)), Position(140, 1)))  # Lento

print(partitura.tempo_sequence)
print('--------------')
out = []
for i in range(60):
    out.append(round(f.eval(i+140)))
print('Rall = {}'.format(out))

[0, Tempo(Tempo[48, 1/4])], [20, Tempo(Tempo[120, 1/4])], [35, Tempo(Tempo[92, 1/4])], [50, [TempoFctn(<main.PiecewiseLinearFunction object at 0x15036f6b0>) per 1/4 note]], [100, Tempo(Tempo[200, 1/4])], [140, Tempo(Tempo[48, 1/4])]
--------------
Rall = [200, 197, 195, 192, 190, 187, 185, 182, 180, 177, 175, 172, 170, 167, 165, 162, 159, 157, 154, 152, 149, 147, 144, 142, 139, 137, 134, 132, 129, 127, 124, 121, 119, 116, 114, 111, 109, 106, 104, 101, 99, 96, 94, 91, 89, 86, 83, 81, 78, 76, 73, 71, 68, 66, 63, 61, 58, 56, 53, 51]

Lo stesso per crescendo e diminuendo:

• Dynamics per definire i cambiamenti di tempo repentini.
• DynamicsFunctionEvent per quelli che si svolgono attraverso qualche tipo di interpolazione. Gli argomenti sono:
  • la funzione da impiegare.
  • la posizione di inizio dell'accelerando o ritardando.

In questo caso i valori nelle interpolazioni devono essere velocity che possiamo recuperare attraverso il metodo dedicato.

partitura = Score()

catalogo = InstrumentCatalog.instance()
partitura.add_instrument_voice(InstrumentVoice(catalogo.get_instrument('violin'))) # Aggiunge 1 violino
vl = partitura.get_instrument_voice('violin')[0]                                   # Recupera 1 voce


vl.voice(0).dynamics_sequence.add(DynamicsEvent(Dynamics.P, Position(0, 1)))     # Piano
vl.voice(0).dynamics_sequence.add(DynamicsEvent(Dynamics.FF, Position(20, 1)))   # Fortissimo
vl.voice(0).dynamics_sequence.add(DynamicsEvent(Dynamics.MF, Position(35, 1)))   # Mezzoforte

cresc = [(Position(50,1), Dynamics.MF.velocity), (Position(100, 1),Dynamics.FFF.velocity)] # Crescendo (in Velocity MIDI)
f = PiecewiseLinearFunction(cresc)
vl.voice(0).dynamics_sequence.add(DynamicsFunctionEvent(f, Position(50,1)))                   
  
vl.voice(0).dynamics_sequence.add(DynamicsEvent(Dynamics.MF, Position(100, 1)))   # Fortissimissimo

dim = [(Position(140,1), Dynamics.FFF.velocity), (Position(200, 1),Dynamics.MP.velocity)]   # Diminuendo (in Velocity MIDI)
f = PiecewiseLinearFunction(dim)
vl.voice(0).dynamics_sequence.add(DynamicsFunctionEvent(f, Position(140,1)))                    
vl.voice(0).dynamics_sequence.add(DynamicsEvent(Dynamics.MP, Position(140, 1)))   # Mezzopiano

print(vl.voice(0).dynamics_sequence)
print('--------------')
out = []
for i in range(60):
    out.append(round(f.eval(i+140)))
print('Dim = {}'.format(out))

[0, Dynamics(P)], [20, Dynamics(FF)], [35, Dynamics(MF)], [50, [DyFctn(<main.PiecewiseLinearFunction object at 0x15030fa40>)]], [100, Dynamics(MF)], [140, Dynamics(MP)]
--------------
Dim = [120, 119, 118, 117, 116, 115, 114, 113, 113, 112, 111, 110, 109, 108, 107, 106, 105, 104, 103, 102, 101, 100, 99, 99, 98, 97, 96, 95, 94, 93, 92, 91, 90, 89, 88, 87, 86, 85, 85, 84, 83, 82, 81, 80, 79, 78, 77, 76, 75, 74, 73, 72, 71, 71, 70, 69, 68, 67, 66, 65]

Musica

Crescendo e diminuendo

Possiamo inserirli sotto forma simbolica attraverso forcelle.

\version "2.24.3"
\language "english"

\relative c'{ 
             c1\p\<~ c 
             c'\mf \> ~ c c'\p 
             }

Oppure in forma testuale.

\relative c'{ 
             c1\p\cresc~ c 
             c'\mf \dim ~ c c'\p 
             }

In entrambe i casi dobbiamo specificare la nota che chiude la forcella attraverso il simbolo \!

Se presente un nuovo crescendo o diminuendo oppure una nuova indicazione dinamica non serve \! .

Accelerando e ritardando

In questo caso possiamo specificarli come testo e aggiungere o meno i trattini estensori (spanner)

\relative c'' {
               \override TextSpanner.bound-details.left.text = "rit." % Testo da visualizzare
               b1 \startTextSpan
               c
               e, \stopTextSpan
               }

Anche in questo caso dobbiamo indicare la fine dei trattini.

Suono

Crescendo e diminuendo

In tutte le DAW possiamo controllare i cambiamenti dinamici attraverso automazioni.

In Audacity dobbiamo selezionare il cursore apposito

per poi definire i punti nei soundfiles caricati nelle tracce da modificare.

Possiamo modificare la curva delle rampe disegnandola attraverso più punti.

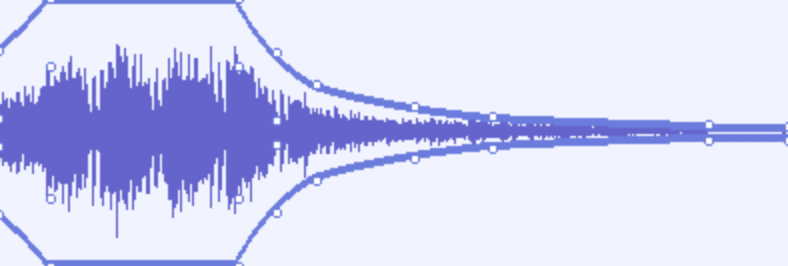
Accelerando e ritardando

Per quanto riguarda questi parametri possiamo creare una traccia temporale.

$\rightarrow$ Tracce $\rightarrow$ Aggiungi nuova $\rightarrow$ Traccia temporale.

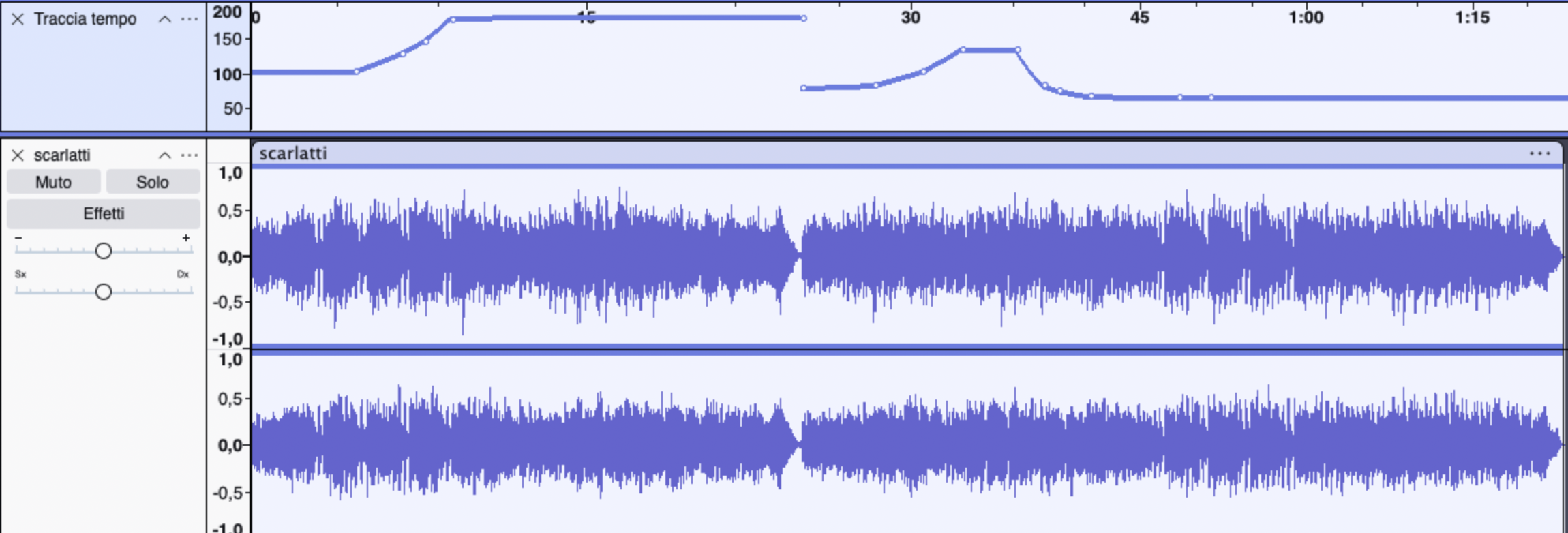
In questo caso sull'asse delle x sono specificati i tempi in bpm e l'azione non è distruttiva.

Con questa tecnica però si modificano anche le altezze.

Se non vogliamo modificare le altezze dobbiamo applicare un effetto distruttivo.

• selezionare con il cursore inizio e fine dell'accelerando o ritardando
• $\rightarrow$ Effetti $\rightarrow$ Intonazione e tempo $\rightarrow$ Allungamento mobile.