Ampiezza e inviluppi¶
Indice¶
Ampiezza e inviluppi ¶
Nel paragrafo precedente abbiamo modificato l'intensità di un segnale moltiplicando il valore di ogni campione (ampiezza tra -1.0 e +1.0) per una costante compresa tra 0.0 e 1.0 chimata anch'essa ampiezza.
0.0 genera silenzio e 1.0 mantiene l'intensità del segnale originale.
Il termine ampiezza risulta dunque troppo generico.
Per evitare confusione aggiungiamo un aggettivo per distinguere tre differenti modalità di misurazione.
import numpy as np
import os
import sys
sys.path.insert(0, os.path.abspath('moduli'))
import parametri as par
%matplotlib inline
Tipi di ampiezza ¶
Ampiezza istantanea - La misura del valore di energia in un preciso istante nel tempo. Valori compresi tra -1.0 e 1.0. Nella rappresentazione dei segnali su un piano cartesiano, il valore misurato sull'asse delle ordinate (y) in un punto preciso sull'asse delle ascisse (x). Nell'audio digitale è il valore di un singolo campione.
Ampiezza di picco - il valore assoluto di energia più alto tra le ampiezze istantanee comprese in un tempo finito. Valori compresi tra 0.0 e 1.0. Se il Valore più alto è negativo togliamo il meno.
Root Mean Square (RMS) - una particolare media dei valori di energia delle ampiezze istantanee comprese in un tempo finito. Valori compresi tra 0.0 e 1.0.
- insieme finito di ampiezze istantanee - ( 0.0, 1.5, 1.0, 0.4, 0.6, 0.0, -0.4, -0.2, -1.0, -1.5, 0.0 )
- elevate al quadrato (square) - ( 0.0, 2.25, 1.0, 0.16, 0.36, 0.0, 0.16, 0.04, 1.0, 2.25, 0.0)
- media matematica (mean) - 0.65636363636364
- radice quadrata (root) - 0.81016272215132
n = 12 # Numero di valori
a = par.amp(n) # Valori ampiezza istantanea
print('Ampiezze istantanee: ' + str(a))
a = np.abs(a) # Valori assoluti
a = np.amax(a) # Restituisce il valore più alto
print('Ampiezza di picco: ' + str(a))
a = par.amp(n) # Valori ampiezza istantanea
a = a**2 # Eleva al quadrato
a = np.mean(a) # Calcola la media aritmetica
a = np.sqrt(a) # Calcola la radice quadrata
a = np.round_(a, 2) # Approssima a due decimali
print('Root Mean Square: ' + str(a))
par.img(n)
Ampiezze istantanee: [ 0. 0.86 0.65 0.34 0.59 0.34 -0.61 -0.85 -0.21 -0.04 -0.34 0.03] Ampiezza di picco: 0.86 Root Mean Square: 0.5
La principale differenza tra ampiezza di picco e RMS sta nel fatto che la prima è un valore univoco indipendente dall'andamento del segnale mentre la seconda essendo una media è strettamente legata all'andamento dell'inviluppo del segnale.
par.sf('6_ampiezza/media/pizz.wav')
par.sf('6_ampiezza/media/tenuto.wav')
Ampiezza di picco: 0.88 Root Mean Square: 0.12
Ampiezza di picco: 0.91 Root Mean Square: 0.25
Variazioni di ampiezza ¶
In musica è importante misurare non solo le ampiezze ma anche i rapporti che intercorrono tra suoni con intensità differenti.
Questo parametro è anche comunemente chiamato volume o fattore di amplificazione e possiamo rappresentarlo in due diversi modi:
- Simboli musicali - I valori sono quasi sempre relativi al contesto musicale, ovvero un "forte" in una sonata per violino barocca non ha la stessa intensità di un "forte" dato agli ottoni in un poema sinfonico di R.Strauss. A differenza delle altezze dove esiste una corrispondenza precisa tra la rappresentazione simbolica in notazione musicale e la misurazione fisica, le dinamiche musicali sono caratterizzate da una rilevante soggettività che va ben oltre alla semplice misura fisica delle ampiezze dei suoni.

- Valori numerici relativi a diverse unità di misura che si riferiscono tutte all'ampiezza di picco:
Lineare - Unità di misura assoluta espressa in valori decimali compresi tra 0.0 e 1.0. La più lontana dalla percezione umana riguardo i cambiamenti di intensità dei suoni. Un suono con ampiezza di 0.5 sarà sempre la metà del suono "più forte possibile" e avrà sempre la stessa intensità indipendentemente dal contesto musicale.
Key Velocity (MIDI) - Unità di misura assoluta espressa in valori interi compresi tra 0.0 e 1.0. La meno precisa a causa del limitato numero di livelli dovuto alla disponibilità di soli 7 bit del protocollo MIDI. Un suono con una key velociy di 127 sarà sempre "il più forte possibile" e avrà sempre la stessa intensità indipendentemente dal contesto musicale.
Quartica - Unità di misura assoluta espressa in valori decimali compresi tra 0.0 e 1.0. La più vicina alla percezione umana riguardo i cambiamenti di intensità dei suoni. Per calcolare i valori corretti dobbiamo elevare l'ampiezza lineare alla quarta potenza. Essendo compresi tra 0.0 e 1.0 l'ambito (range) rimane lo stesso.
$$a^4$$Decibels (dB) - Unità di misura relativa espressa in valori decimali compresi tra 0.0 e -inf (o +inf a seconda del tipo di misurazione). Misura la differenza di intensità tra l'ampiezza di un suono rispetto a un'ampiezza di riferimento. Un suono con ampiezza di -6.02 dB sarà sempre forte la metà rispetto a un suono la cui ampiezza è stata presa come riferimento per la misurazione. Per calcolare i valori corretti dobbiamo utilizzare la seguente formula dove $a$ è il valore dell'ampiezza lineare del suono che vogliamo misurare mntre $a0$ è l'ampiezza del suono di riferimento (1.0).
$$20*\log_{10}(\frac{a}{a0})$$
par.curve()
| Segno | Vel | lin | quart | dB | |
|---|---|---|---|---|---|
| pppp | 12 | 0.1 | 0.0001 | -20 | |
| ppp | 24 | 0.2 | 0.0016 | -14 | |
| pp | 44 | 0.3 | 0.0081 | -10 | |
| p | 54 | 0.4 | 0.0256 | -8 | |
| mp | 64 | 0.5 | 0.0625 | -6 | |
| mf | 74 | 0.6 | 0.1296 | -4 | |
| f | 84 | 0.7 | 0.2401 | -3 | |
| ff | 94 | 0.8 | 0.4096 | -2 | |
| fff | 114 | 0.9 | 0.6561 | -1 | |
| ffff | 127 | 1.0 | 1.0000 | 0 |
Conversioni di ampiezza ¶
Gli oggetti dedicati all'ampiezza e alle sue variazioni nel tempo dei diversi software musicali accettano generalmente valori di ampiezza lineare (tra 0.0 e 1.0) e/o decibels (tra -inf. e 0.0).
Potremmo anche in questo caso avere la necessità di convertire i valori da un'unità di misura ad un'altra.
Formule
Da ampiezza lineare a MIDI velocity e viceversa
$vel = amp_{lin} * 127$
$amp_{lin} = vel / 127$
Da ampiezza lineare ad ampiezza quartica e viceversa
$amp_{q} = amp_{lin}^4$
$amp_{lin} = \sqrt[4]{amp_{q}}$
Da ampiezza lineare a decibels e viceversa
$dB = 20 * log_{10}(amp_{lin})$
$amp_{lin} = 10^{(dB/20)}$
In SuperCollider
a = 0.5;
v = a * 127;
v = 64;
a = v / 127;
a = 0.5;
q = a**4;
q = 0.0625;
a = pow(q, 1/4); // radice ennesima di x = x**(1/radice ennesima)
a = 0.5;
d = 20 * log10(a);
d = -12;
a = 10**(d/20);
In Pure Data
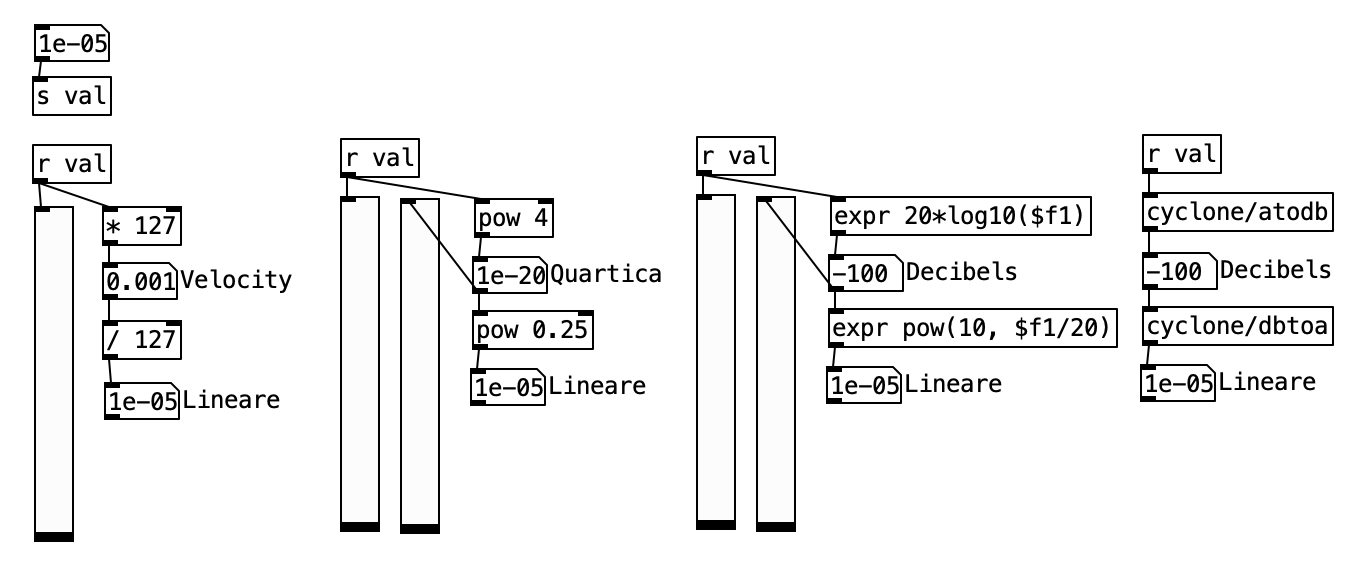
os.system('open 6_ampiezza/patch/6.1.pd')
0
Interpolazioni e rampe¶
Quando controlliamo i parametri di uno strumento possiamo farlo principalmente in due modi.
- cambio repentino - il nuovo valore si aggiorna nel momento stesso in cui viene ricevuto.
- rampe - il nuovo valore viene raggiunto gradualmente dopo un numero finito di passi (interpolazione).
Un'interpolazione ci permette di realizzare il seguente concetto.
vai da a fino a b in n_passi
(
a = 0.1; // Inizio
b = 1.0; // Fine
n = 10; // Numero di passi
i = Array.interpolation(n, a, b); // Interpolazione
i.postln;
i.plot.plotMode_(\points);
)
// 1 2 3 4 5 6 7 8 9 10 Passi
// [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0] Valori
Una variante del concetto precedente spesso impiegata in musica nel sostituire 'a' con l'ultimo valore raggiunto (stato):
(dal valore raggiunto) vai fino a b in n_passi
a = 0.1; // Valore di init (fuori dal blocco di codice)
(
b = rand(50); // Vai a questo valore
n = 6; // in n passi
i = Array.interpolation(n, a, b);
i.postln;
i.plot(minval:0,maxval:50).plotMode_(\points);
a = b; // L'ultimo valore diventa quello di partenza
)
// 1 2 3 4 5 6 Passi
// [0.1, 7.88, 15.66, 23.44, 31.22, 39.0] Valori
In entrambe i casi il delta o incremento del valore a ogni passo è costante in quanto si tratta di interpolazioni lineari.
In informatica musicale usiamo un tipo di interpolazioni chiamate rampe dove il numero di passi per andare da un valore all'altro è legato al tempo e corrisponde a un numero finito di campioni.
Il concetto delle rampe è:
vai da a fino a b in tot_tempo
Il numero di passi corrisponde alla rata di campionamento per il tempo specificato.
Esempio: vai da 0.0 a 1.0 in 1 secondo.
Se la rata di campionamento è 44.100 Hz i passi saranno 44.100 e il valore incrementale (delta) a ogni campione di 1/44.100 mentre se è 48.000 i passi saranno 48.000 e il valore incrementale più piccolo (1/48.000).
La rampa andrà comunque da 0.0 a 1.0 in un secondo.
Avrà semplicemente più o meno definizione.
In SuperCollider possiamo realizzare interpolazioni nell'Interprete mentre e rampe nel Server.
In PD ci sono oggetti sia per generare interpolazioni (controllo) che rampe (audio).
Interpolazioni non lineari
Ci sono due tipi di interpolazioni:
- lineari - il fattore incrementale rimane costante ad ogni passo.
- non lineari - logaritmiche o esponenziali dove il fattore incrementale aumenta o diminuisce a ogni passo
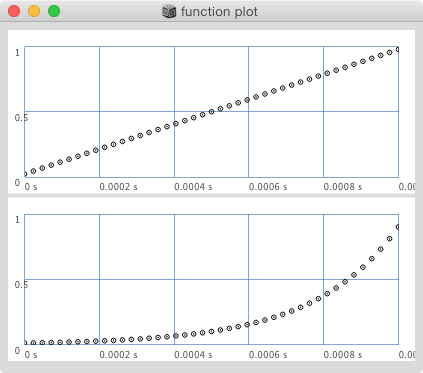
Nelle interpolazioni non lineari se i valori sono compresi tra 0.0 e 1.0 cambia la curva ma non inizio e fine, se invece il range è compreso tra altri valori inizio e/o fine vengono riscalati a seconda dell'esponente o della base logaritmica.
doneAction in SuperCollider¶
In SuperCollider possiamo utilizzare la UGen ___Line.ar()___ per generare rampe lineari e la UGen ___XLine.ar()___ per rampe esponenziali.
Per entrambe gli argomenti sono: Line.ar(inizio, fine, durata).
Per XLine-ar() inizio e fine non possono essere 0.0 e devono avere lo stesso segno.
(
SynthDef(\myLine, {arg a=0,b=1,dur=1
var rampa;
rampa = Line.ar(a,b,dur);
//rampa = XLine.ar(a,b,dur);
Out.ar(0, rampa)
}).add;
)
a = Synth(\myLine);
//a = Synth(\myLine. [0.001, 1, 1]); // Se XLine..
a.set(\a,1, \b,0.001, \dur,0.5); // se eseguiamo non accade nulla...
Se proviamo a modificare dinamicamente uno dei parametri invocando ___.set()___ la rampa non si ripete in quanto viene generata solo alla creazione del Synth.
Questa è una importante limitazione di queste UGens che le differenzia dagli oggetti omonimi di Max.
Uno degli argomenti comuni ad alcune UGens è ___doneAction:n___ che si rivela estremamente utile per l'allocazione dinamica delle voci (dynamic voice allocation) e per risparmiare risorse della CPU.
Possiamo assegnare a questo argomento un valore compreso tra 0 e 14.
Ognuno di questi rappresenta un'azione automatica che ha effetto sul Synth che contiene la UGen nella quale è specificato questo argomento quando questa ha terminato il suo compito (nel caso di Line al termine della rampa).

Tra tutte queste possibilità quelle che sono più utilizzate sono ___doneAction:0___
(
{[SinOsc.ar,
Line.ar(0, 1, 1, doneAction:0),
SinOsc.ar*Line.ar(0, 1, 1, doneAction:0)
]}.plot(2);
)
{SinOsc.ar*Line.ar(0, 1, 1, doneAction:0).scope}.scope
e ___doneAction:2___
(
{[SinOsc.ar,
Line.ar(0, 1, 1, doneAction:2),
SinOsc.ar*Line.ar(0, 1, 1, doneAction:2)
]}.plot(2);
)
{SinOsc.ar*Line.ar(0, 1, 1, doneAction:2).scope}.scope
line e curve in Pure Data¶
In PD possiamo realizzare rampe di diverso tipo con gli oggetti line (vanilla), line~ e curve~ (cyclone).
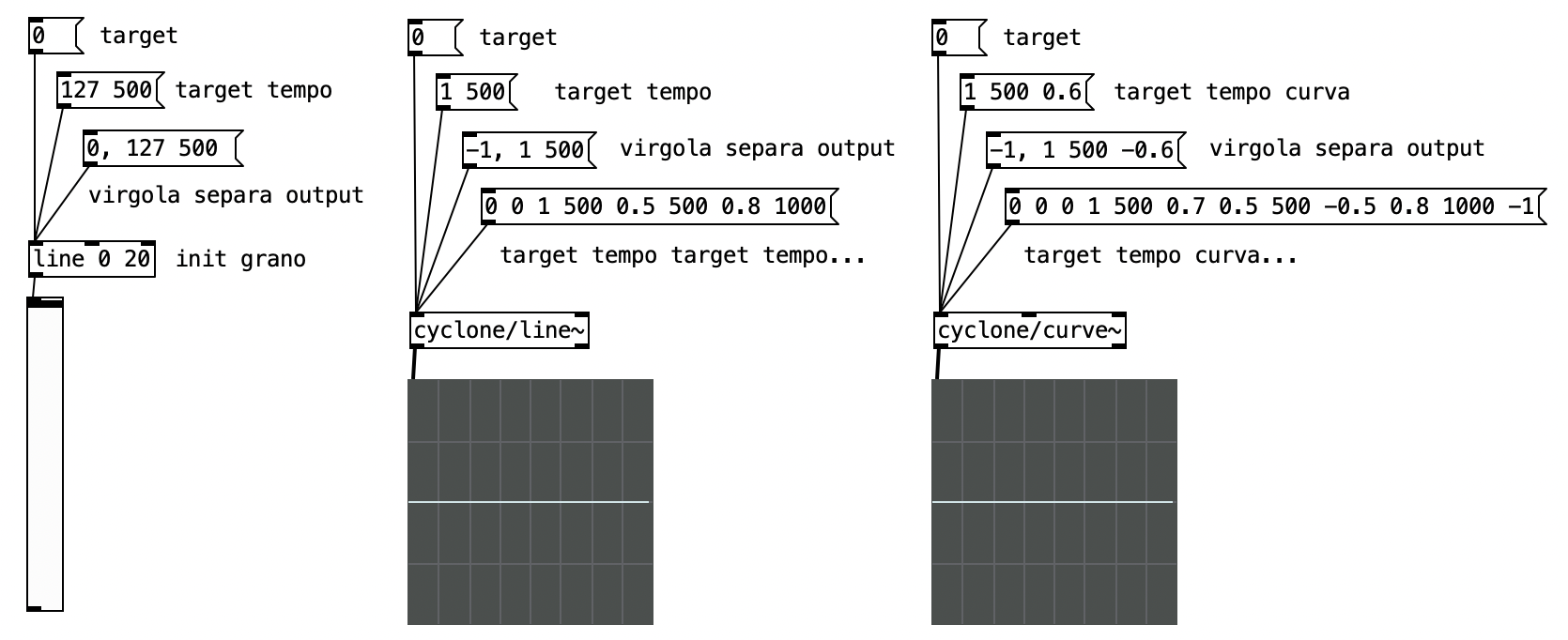
os.system('open 6_ampiezza/patch/6.2.pd')
0
Per quanto riguarda il terzo argomento di curve~:
- logaritmico - tra -1.0 e 0.0
- lineare - 0.0
- esponenziale - tra 0.0 e 1.0
Dall'outlet destro esce un bang alla fine della rampa.
BPF e segnali di controllo ¶
Nel paragrafo precedente abbiamo osservato rampe di un solo segmento.
Per generare rampe multisegmento possiamo definire i diversi punti su un piano cartesiano specificandone le coordinate (xy) dove le ascisse (x) corrispondono al tempo mentre le ordinate (y) ai livelli.
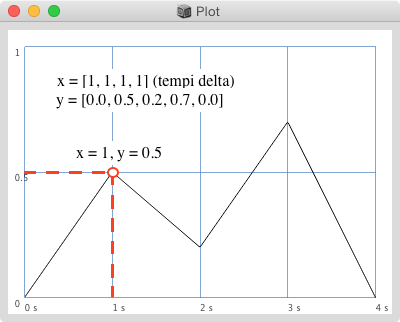
Questo tipo di descrizione e visualizzazione si chiama BPM (Break Point Function) e in quasi tutti i software musicali è presente un'interfaccia grafica che ci permette di definire e visualizzare tutti i segmenti multirampa che desideriamo.
In SuperCollider la classe Env mentre in Max l'oggetto function.
Env ed EnvGen in SuperCollider ¶
La classe ___Env___ ci permette di definire tutte le tipologie di inviluppi che desideriamo sotto forma di BPF.
Il metodo ___.new___ (che ricordiamo può essere sottinteso) crea un nuovo inviluppo (istanza).
I suoi primi due argomenti sono:
- livelli (valori y - rossi nella figura) sotto forma di Array.
- tempi delta (valori x - blu nella figura) in secondi sotto forma di Array con un elemento in meno rispetto i livelli.
Il metodo ___.test___ serve come monitor uditivo.
Il metodo ___.plot___ come monitor visivo.
s.boot; // Per il metodo .test
(
Env.new([0, 0.7, 0.1, 0], // Livelli
[ 0.1, 0.2, 1 ] // Tempi delta
).test.plot(minval: 0, maxval: 1);
)

Possiamo anche specificare un terzo argomento che ne specifica la curva in due modi.
- attraverso un simbolo
(
[Env([0,0.5,0.1,0], [0.1,0.2,1], \step), // Scalini
Env([0,0.5,0.1,0], [0.1,0.2,1], \lin), // Curva lineare
Env([0.0001,0.5,0.1,0.0001],[0.1,0.2,1], \exp), // Curva esponenziale
Env([0,0.5,0.1,0], [0.1,0.2,1], \sin), // Curva sinusoidale
Env([0,0.5,0.1,0], [0.1,0.2,1], \wel), // Curva welch
Env([0,0.5,0.1,0], [0.1,0.2,1], \sqr), // Curva radice
Env([0,0.5,0.1,0], [0.1,0.2,1], \cub)].plot; // Curva quartica
)
- attraverso il valore di curvatura come nell'oggetto curve~ di Max.
(
[Env([0,0.5,0.1,0],[0.1,0.2,1], -0.8), // Curva logaritmica_n
Env([0,0.5,0.1,0],[0.1,0.2,1], 0.0), // Curva lineare
Env([0,0.5,0.1,0],[0.1,0.2,1], 0.8)].plot // Curva esponenziale_n
)
Possiamo specificare curve diverse, una per ogni segmento sotto forma di Array.
(
[Env([0,0.5,0.1,0], [0.1,0.2,1], [ 2, 0, -8]),
Env([0,0.5,0.1,0], [0.1,0.2,1], [\lin,\exp,\sqr])].plot;
)
Una Break Point Function descrive punti su un piano cartesiano non rampe.
Dobbiamo generare i valori intermedi tra i punti attraverso interpolazioni che trasformino le BPF in segnali di controllo.
Così facendo potremo moltiplicare tra loro i valori dei singoli campioni del segnale al quale vogliamo applicare l'inviluppo con i valori delle rampe generate dall'inviluppo.
La UGen ___EnvGen___ svolge questo compito.
(
{EnvGen.kr( // Anche .ar
Env.new([0,0.5,0.1,0],[0.01,0.2,1],\cub), // BPF
1, // Gate (1 = noteon, 0 = noteoff)
doneAction:2) // doneAction
}.scope;
)
Esempio di inviluppo d'ampiezza.

(
SynthDef(\envi,
{arg freq=500, amp=0, gate=0, done=2;
var sig, env;
sig = SinOsc.ar(freq);
env = Env.new([0,1,0.5,0], [0.01,0.2,1], \cub);
env = EnvGen.kr(env, gate, doneAction:done);
sig = sig * env * amp;
Out.ar(0,sig)
}
).add
)
Synth(\envi,[\freq,rrand(200,2000), \amp, rand(1.0), \gate,1]);
Messaggi e function in Pure Data ¶
Per la definizione grafica di un inviluppo in PD possiamo utilizzare l'oggetto function che genera una lista di valori come quella che abbiamo definito a mano.
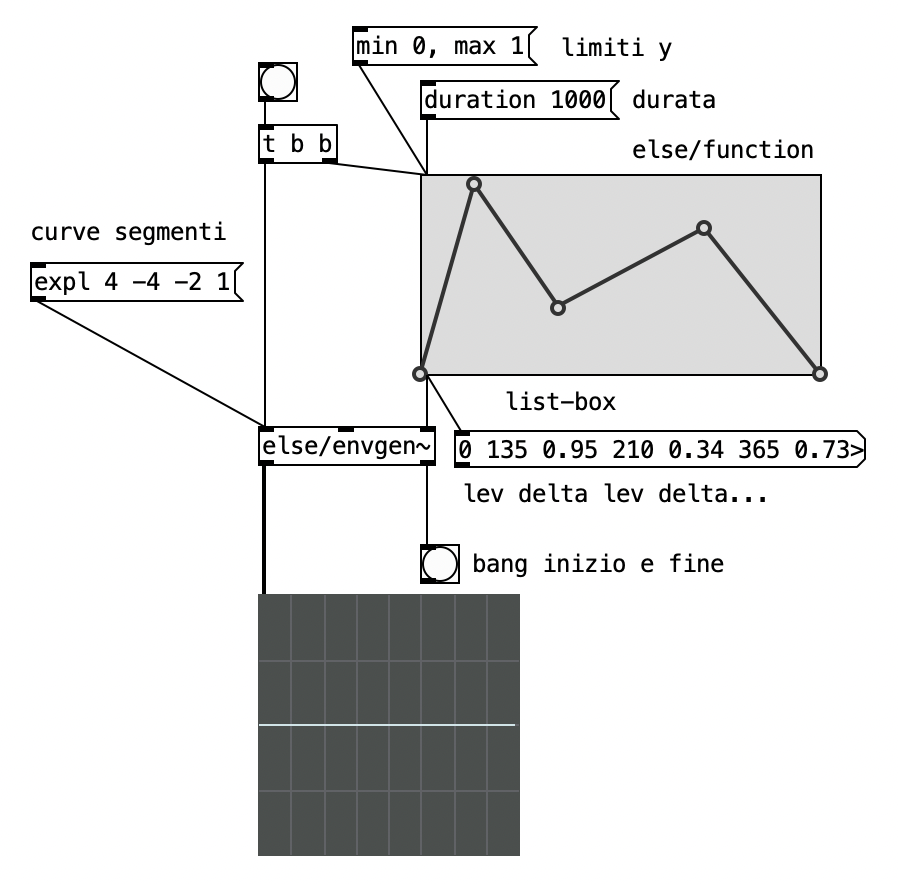
os.system('open 6_ampiezza/patch/6.3.pd')
0
Trigger e tipologie di inviluppi ¶
Un trigger è il comando che fa partire una qualsiasi azione o evento come l'invio della nuova frequenza di una nota, l'avvio di una sequenza di note o di un suono, l'invio di parametri di controllo a un Synth oppure la partenza di un inviluppo.
Esistono due tipologie di inviluppi che si distinguono tra loro in base al numero di triggers necessario per realizzarsi.
inviluppi senza fase di sostegno - pensiamo a un tamburo o a uno strumento a percussione: il suono (il suo inviluppo d'ampiezza) comincia nel momento in cui la bacchetta o le mani colpiscono la pelle dello strumento (trigger) dopodichè il suono termina dopo un tot di tempo (durata) con l'esaurirsi delle vibrazioni dello strumento.
E' necessario un solo trigger iniziale (gate:1) e dobbiamo specificare la durata del suono.
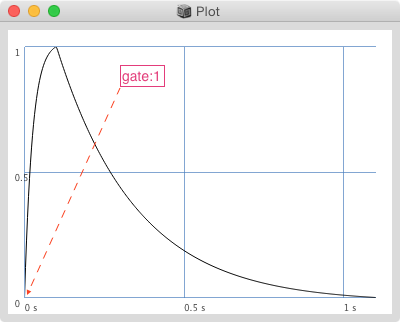
inviluppi con fase di sostegno - pensiamo a una tastiera: quando premiamo un tasto (note On) facciamo partire l'inviluppo dopodichè il suono continua (fase di sostegno) fino a quando non rilasciamo il tasto (note Off) facendo partire il rilascio del suono fino all'estinzione.
In questo caso sono necessari due triggers:
- gate:1 - fa partire l'inviluppo.
- gate:0 - fa partire il rilascio del suono.
e non possiamo specificare la durata del suono.

Sviscereremo le caratteristiche di entrambi in paragrafi dedicati.
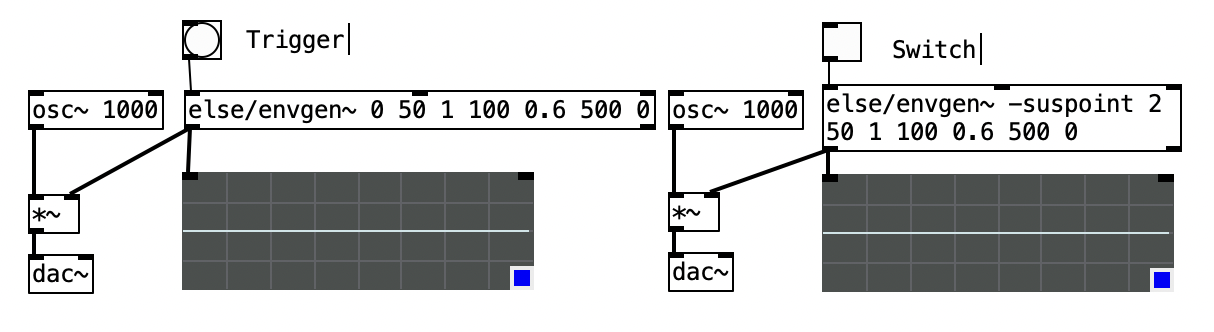
os.system('open 6_ampiezza/patch/6.4.pd')
0
Inviluppi senza fase di sostegno¶
Per definire gli inviluppi senza fase di sostegno dobbiamo stabilire:
- durata totale del suono.
- profilo dell'inviluppo (costituito da):
- livelli di partenza e di arrivo di ogni rampa.
- tempi delta di ogni rampa.
- curva di ogni rampa.
- trigger ('note on' oppure 'gate:1' oppure '1')
A seconda delle caratteristiche del software di realizzazione potremmo dover effettuare una serie di operazioni per ottimizzare la manipolazione di questi parametri in modo musicale.
SuperCollider¶
In SuperCollider possiamo definire qualsiasi profilo di inviluppo invocando il metodo .new() sulla classe Env oppure utilizzare altri metodi che richiamano i profili di tipologie classiche.
Env.new¶
Invocando il metodo ___.new()___ sulla classe ___Env___ generiamo un'istanza di un inviluppo custom che possiamo disegnare a piacere definendone tutti i parametri (livelli, tempi_delta, curve).
Può essere sia con che senza fase di sostegno.
Nella sua versione senza fase di sostegno i suoi argomenti sono:
s.boot;
// livelli tempi delta curva
Env.new([0, 1, 0.65, 0.8, 0],[0.3, 0.8, 0.5, 1], \sine).test.plot;
Env.new([0, 1, 0.65, 0.8, 0],[0.3, 0.8, 0.5, 1], [0.9, 0.6, 0, -0.7]).test.plot;
t_gate¶
Potremmo pensare che per questo tipo di inviluppi sia superfluo inviare il messaggio ___gate:0___ (note off) in quanto terminano il loro percorso automaticamente.
Non è così.
Per convenzione infatti in quasi tutti i software dobbiamo sempre fare seguire un messaggio di note off dopo uno di note on anche quando sembra superfluo.
(
SynthDef(\envi,
{arg freq=980, amp=0, gate=0, done=0;
var sig, env;
sig = SinOsc.ar(freq);
env = Env.new([0,1,0.3,0],[0.01,0.2,0.3],\cub);
env = EnvGen.kr(env, gate, doneAction:done);
sig = sig * env * amp;
Out.ar(0, sig)
}
).add;
)
a = Synth(\envi);
a.set(\freq, 967, \amp, 0.5, \gate,1); // Se valutiamo nuovamente prima di gate 0 non va
a.set(\gate,0);
a.set(\freq, 893, \amp, 0.5, \gate,1);
a.set(\gate,0);
Questo meccanismo rende piuttosto macchinoso il controllo musicale e la programmazione di sequenze con questo tipo di inviluppi.
Se però facciamo precedere t_ al nome dell'argomento assegnato a gate, SuperCollider genera il messaggio di gate:0 (note Off) automaticamente alla fine della rampa.
(
SynthDef(\envi,
{arg freq=980, amp=0, t_gate=0, done=0;
var sig, env;
sig = SinOsc.ar(freq);
env = Env.new([0,1,0.3,0],[0.01,0.2,0.3],\cub);
env = EnvGen.kr(env, t_gate, doneAction:done);
sig = sig * env * amp;
Out.ar(0, sig)
}
).add;
)
a = Synth(\envi);
a.set(\amp, 0.5, \t_gate,1);
Array¶
Livelli e tempi delta di Env.new sono specificati sotto forma di Array.
Un array è una collezione indicizzata di dati di qualsiasi tipo (numeri, UGens, Env, etc.).
In SuperCollider sono inclusi tra parentesi quadre e separati da virgole.
Ad ogni elemento corrisponde un indice sottinteso che parte da 0.
// 0 1 2 3 4 Indici sottintesi
a = [34, 45.4, "ciao", Env.new, SinOsc.ar]; // Elementi (items)
a.postln;
Gli array sono impiegati per molti propositi, possiamo modificarne il contenuto in diversi modi invocando metodi dedicati ed effettuare operazioni matemetiche ma non possiamo modificarne il numero di elementi dinamicamente.
a = [10, 20, 30, 40];
a.put(0, 23); // Sostituisci il 10 all'indice 0 con 23
b = a.reverse; // Inverte l'ordine
c = a * 100; // Moltiplica tutti gli elementi per 100
Esiste un particolare tipo di array che si chiama literal array sul quale possiamo effettuare tutte le operazioni che vogliamo ma del quale non possiamo modificarne il contenuto ed è identificato con un # prima della parentesi di apertura.
a = #[10, 20, 30, 40];
a.put(0, 23); // Dà errore
Quando un array contiene valori numerici, possiamo visualizzarli in un piano cartesiano invocando il metodo .plot().
Gli indici (sottintesi) rappresentano le ascisse (x) e i valori (elementi) le ordinate (y).
#[12,34,56,3,78,98,23,9].plot; // valori determinati
Questo metodo come molti altri può essere invocato su diversi tipi di oggetti (polimorfismo), tra i quali gli Array.
Se richiamiamo l'Help file di un metodo compare un elenco di oggetti sui quali può essere invocato.

L’aspetto di un plot è personalizzabile attraverso gli argomenti.
Prestiamo attenzione che a seconda del tipo di data sul quale è invocato, gli argomenti di un metodo possono cambiare.
Nell’esempio seguente sono presenti quelli spendibili nella visualizzazione di Array numerici.
(
a = #[12,34,56,3,78,98,23,9];
a.plot(name: "mio plot", // Nome
bounds:540@200, // Dimensioni x@y in pixels
minval: -100, // Valore limite inferiore
maxval: 100, // Valore limite superiore
discrete:true) // True = punti, false = linee
)
E' sempre raccomandabile specificare minval e maxval perchè di default i limiti si adattano ai valori contenuti nell’array e questo potrebbe generare errori di lettura e valutazione.
Confrontiamo le seguenti visualizzazioni.
(
a = #[0.1,0.5,0.6,0.1,0.9,0.3];
b = #[1,5,2,4,8,10,5,6];
[a, b].plot;
[a, b].plot(minval:0,maxval:10);
)
Durate assolute e segmenti proporzionali¶
Nei paragrafi precedenti la durata delll'evento sonoro è data dalla somma dei tempi delta definiti nell'array dedicato.
Musicalmente è però preferibile definire prima la durata in valori assoluti (secondi o millisecondi) per poi riscalare proporzionalmente le durate delle singole rampe dell'inviluppo.
Per compiere questa operazione dobbiamo fare in modo che la somma dei valori nell'array dei tempi delta sia 1.0 (relativa) in modo da poterli moltiplicare per il valore della durata.
s.boot;
s.plotTree;
s.scope;
(
d = 1.0; // Durata (secondi o ms)
l = [0.0, 1.0, 0.5, 0.8, 0.0]; // Livelli (tra 0.0 e 1.0)
t = [ 0.1, 0.3, 0.2, 0.4 ]; // Tempi - somma = 1.0
t = t * d; // Riscala sulla durata
Env.new(l, t, -4).test.plot;
)
Possiamo definire inviluppi con pochi segmenti effetturando il calcolo a mente mentre se vogliamo pensare in modo proporzionale dobbiamo invocare sull'array dei tempi il metodo [ ].normalizeSum che riscala i valori in modo che la somma dia 1.0.
[10, 30, 50, 90].normalizeSum;
Metodi dedicati¶
Oltre a ___Env.new()___ con il quale possiamo realizzare qualunque tipo di inviluppo SuperCollider fornisce diversi metodi dedicati per la definizione di inviluppi classici principalmente impiegati come inviluppi d'ampiezza.
Anche in questi metodi possiamo riscalare proporzionalmente segmenti e durata.
Env.linen - inviluppo trapezoidale.
// attacco sostegno rilascio livello curva
Env.linen(0.1, 0.2, 0.1, 1, 0 ).test.plot;
Env.linen(1, 2, 3, 0.3, \sine ).test.plot;
Env.linen(1, 2, 3, 1, [[\sine, \welch, \lin, \exp]]).plot; // Array
d = 0.25; // Durata (secondi)
Env.linen(0.1*d, 0.4*d, 0.1*d).test.plot; // La somma deve dare 1.0
(
SynthDef(\trap,
{arg freq=890, t_ciao=0, dur=1, a=0.1, s=0.2, r=0.6, amp=0, done=2;
var sig,env;
sig = SinOsc.ar(freq);
env = Env.linen(a*dur,s*dur,r*dur,amp,-4);
env = EnvGen.kr(env,t_ciao,doneAction:done);
sig = sig * env;
Out.ar(0, sig)
}
).add;
)
w = Synth(\trap, [\done, 0]);
w.set(\dur,rrand(0.1,3.0),\amp,0.5, \t_ciao,1);
(
a = rand(0.5) + 0.01;
u = rand(1-a) + 0.1;
r = 1-a-u; // Somma deve essere 1.0
[a,u,r].postln;
[a,u,r].sum.postln;
w.set(\dur, rrand(0.1,3),
\a, a,
\s, u,
\r, r,
\amp, 0.3,
\t_ciao, 1)
)
Env.perc - inviluppo percussivo
// attacco rilascio livello curva
Env.perc(0.1, 0.9, 1, 0 ).test.plot;
Env.perc(1, 3, 0.3, \sine ).test.plot;
Env.perc(1, 2, 1, [[\sine, \welch]]).plot; // Array
d = 0.25; // Durata (secondi)
Env.perc(0.1*d, 0.9*d).test.plot; // La somma deve dare 1.0
(
SynthDef(\perc,
{arg freq=890, t_ciao=0, dur=1, a=0.1, r=0.6, amp=0, done=2;
var sig,env;
sig = SinOsc.ar(freq);
env = Env.perc(a*dur,r*dur,amp,-4);
env = EnvGen.kr(env,t_ciao,doneAction:done);
sig = sig * env;
Out.ar(0, sig)
}
).add;
)
w = Synth(\perc, [\done, 0]);
w.set(\dur,rrand(0.1,3.0),\amp,0.5, \t_ciao,1);
(
a = rand(0.5) + 0.01;
r = 1-a; // Somma deve essere 1.0
[a,r].postln;
[a,r].sum.postln;
w.set(\dur, rrand(0.1,3),
\a, a,
\r, r,
\amp, 0.3,
\t_ciao, 1)
)
Env.sine - inviluppo sinusoidale
// durata livello
Env.sine(0.1, 1, ).test.plot;
d = 0.25; // Durata (secondi)
Env.sine(d).test.plot;
(
SynthDef(\sine,
{arg freq=890, t_ciao=0, dur=1, amp=0, done=2;
var sig,env;
sig = SinOsc.ar(freq);
env = Env.sine(dur,amp);
env = EnvGen.kr(env,t_ciao,doneAction:done);
sig = sig * env;
Out.ar(0, sig)
}
).add;
)
w = Synth(\sine, [\done, 0]);
w.set(\dur,rrand(0.1,3.0),\amp,0.5, \t_ciao,1);
Env.triangle - inviluppo triangolare
// durata livello
Env.triangle(0.1, 1, ).test.plot;
d = 0.25; // Durata (secondi)
Env.triangle(d).test.plot;
(
SynthDef(\triangle,
{arg freq=890, t_ciao=0, dur=1, amp=0, done=2;
var sig,env;
sig = SinOsc.ar(freq);
env = Env.triangle(dur,amp);
env = EnvGen.kr(env,t_ciao,doneAction:done);
sig = sig * env;
Out.ar(0, sig)
}
).add;
)
w = Synth(\triangle, [\done, 0]);
w.set(\dur,rrand(0.1,3.0),\amp,0.5, \t_ciao,1);
Pure Data¶
In PD possiamo definire inviluppi in due modi:
- con message box (o come argomenti di envgen~)
- con l'oggetto grafico function.
La problematica principale riguarda la diversa sintassi tra i due software.
In SuperCollider due array:
[0., 1., 0.5, 0.] - L Livelli
[ 0.1, 0.2, 0.7 ] - T Tempi
In PD un'unica lista di :
- coppie di Tempi (T) e Livelli (L) se il numero di elementi nella lista è pari (in questo caso possiamo specificare il primo livello come argomento)
- livello iniziale e poi coppie di Tempi (T) e Livelli (L) se il numero di elementi nella lista è dispari.

Se vogliamo riscalare i tempi su una durata assoluta del suono dobbiamo compiere alcune operazioni sulla lista.
Liste e zl¶
In PD le collezioni di dati come gli Array di SuperCollider si chiamano list e possiamo definirle principalmente all'interno di message box.
Così come gli Array di SC gli elementi hanno indici sottintesi.
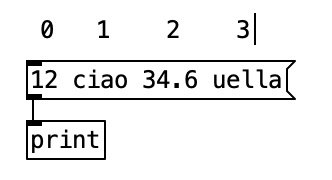
Su di esse possiamo compiere umolte operazioni con diversi oggetti.
Ai fini di una maggiore compatibillità con Max impiegheremo la collezione di oggetti zl della libreria cyclone.
Per calcolare la durata assoluta di un inviluppo dobbiamo sommare tra loro i tempi delta.

os.system('open 6_ampiezza/patch/6.5.pd')
0
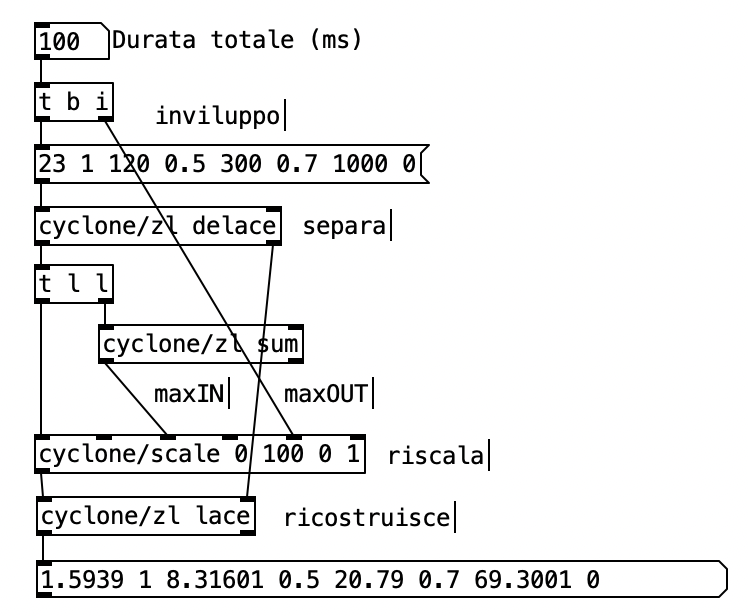
Se invece vogliamo definire una durata e riscalare i tempi delta relativi su di essa dobbiamo:
- separare i livelli dai tempi ottenendo due liste differenti con l'oggetto zl delace.
- riscalare i valori proporzionali in tempi assoluti (tra 0.0 e la durata) con l'oggetto scale.
- ricostruire la lista nella forma sintattica originale con oggetto zl lace.
os.system('open 6_ampiezza/patch/6.6.pd')
0
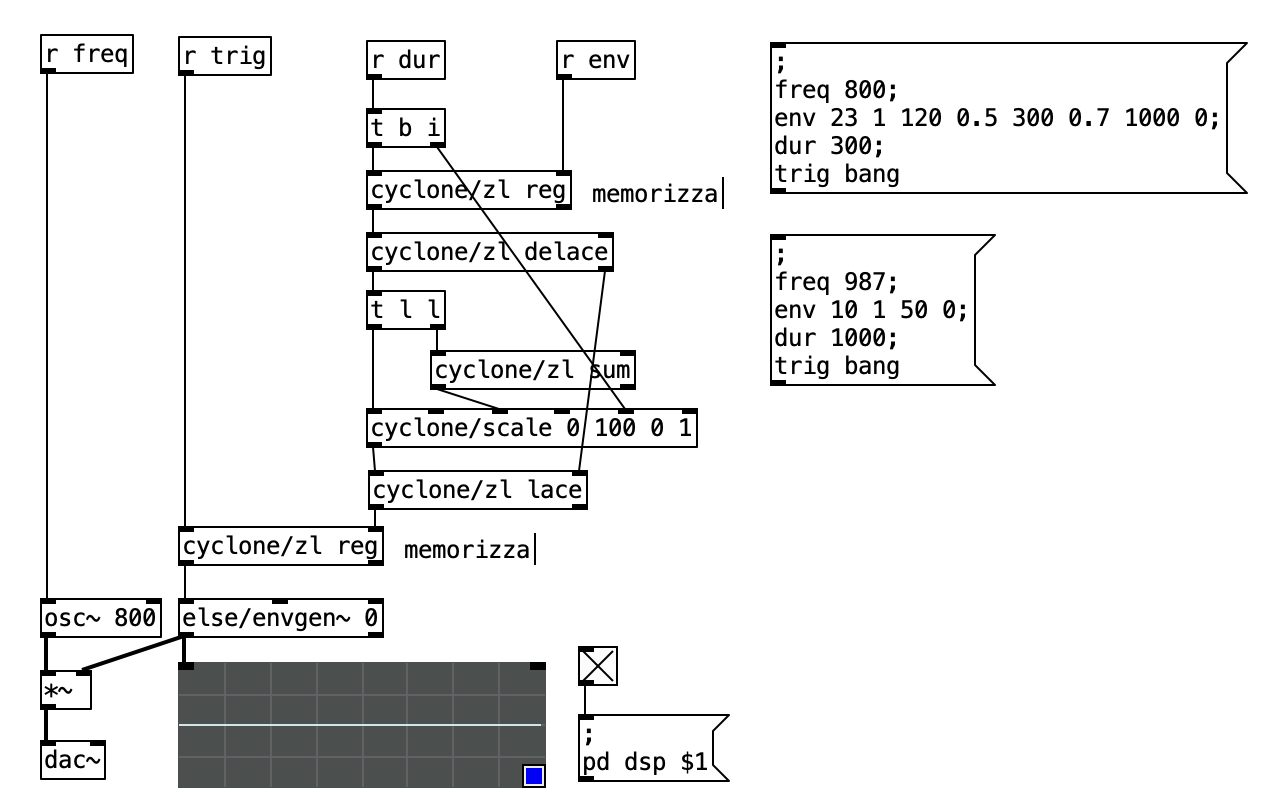
Assembliamo il tutto in un patch.
Notiamo come la struttura sia la stessa delle ___SynthDef___ e del controllo dei parametri in SuperCollider.
os.system('open 6_ampiezza/patch/6.7.pd')
0
Possiamo ottimizzare il patch formalizzandolo subpatches come in precedenza.
Possiamo anche utilizzare la GUI function.

os.system('open 6_ampiezza/patch/6.3.pd')
0
Inviluppi con fase di sostegno¶
Per definire gli inviluppi senza fase di sostegno dobbiamo stabilire:
- durata e numero di segmenti della fase di attacco.
- durata e numero di segmenti della fase di rilascio.
La durata totale non è definita e possiamo definire le durate dei segmenti di attacco e rilascio in valori di tempo assoluto.
SuperCollider¶
Env.new¶
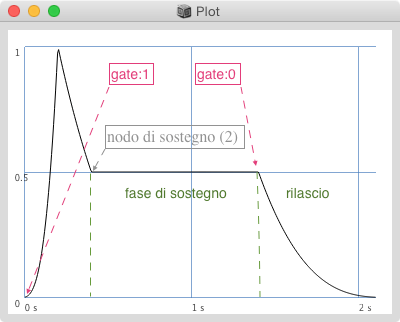
Aggiungiamo un argomento (nodo di sostegno) a quelli che già conosciamo per specificare il numero del nodo di sostegno come indice dell'array dei livelli.
L'inviluppo interrompe il suo corso in questo punto fino a quando non riceve un messggio di ___gate:0___.
s.boot;
s.scope;
s.plotTree;
(
a = Env.new([0,0.8,0.2,0],[0.1,0.2,3],\cub, 2);
a.plot;
a.isSustained; // Riporta se c'è un sustain o meno
)
(
SynthDef(\sust,
{arg freq=935, amp=0, sus=2, gate=0, done=0;
var sig, env;
sig = SinOsc.ar(freq);
// ID 0 1 2 (Nodi)
env = Env.new([0, 0.8, 0.2, 0],[0.1,0.2,3],\cub, sus);
env = EnvGen.kr(env,gate,doneAction:done);
sig = sig * amp * env;
Out.ar(0, sig)
}
).add;
)
a = Synth(\sust, [\amp, 0.5]);
a.set(\gate, 1); // Note on (trigger inizio e si ferma al nodo specificato)
a.set(\gate, 0); // Note off (trigger per proseguire)
Se vogliamo testare questo tipo di inviluppi invocando il metodo ___.test___ possiamo specificare un tempo di ritardo misurato dal trigger iniziale dopo il quale verrà automaticamente generato il messaggio di gate 0:
Env.new([0,0.5,0.05,0],[0.1,1,2], \cub, 1).test(5).plot; // dopo 5" --> gate:0
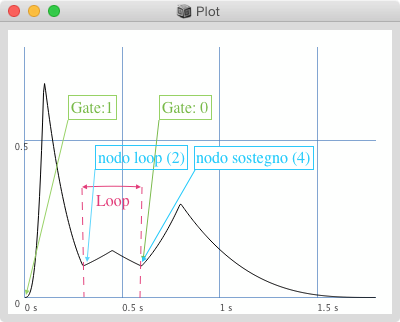
Se aggiungiamo un ulteriore argomento specifichiamo il nodo di loop.
Possiamo utilizzare questo nodo per realizzare un loop tra il nodo di sostegno e questo.
Il suo indice deve essere inferiore al nodo di sostegno.
Il loop prosegue all'infinito fino a quando non riceve un messaggio di gate 0.
a = Env.new([0,0.7,0.1,0.15,0.1,0.3,0], [0.1,0.2,0.15,0.15,0.2,1], \cub, 2, 4).plot;
(
SynthDef(\loop,
{arg freq=935, amp=0, startloop=2, endloop=4, gate=0, done=0;
var sig, env;
sig = SinOsc.ar(freq);
env = Env.new([0,0.7,0.1,0.15,0.1,0.3,0],
[0.1,0.2,0.15,0.15,0.2,1],
\cub,
endloop, startloop);
env = EnvGen.kr(env,gate,doneAction:done);
sig = sig * env * amp;
Out.ar(0, sig)
}
).add;
)
a = Synth(\loop, [\amp, 0.5]);
a.set(\gate,1); // Note on (trigger inizio e si ferma al nodo specificato)
a.set(\gate,0); // Note off (trigger per proseguire)
Metodi dedicati¶
Così come per gli inviluppi senza sostegno in SuperCollider esistono alcuni metodi dedicati che possiamo invocare per realizzare inviluppi ormai classici.
Env.asr - inviluppo trapezoidale (come Env.linen ma con fase di sostegno).
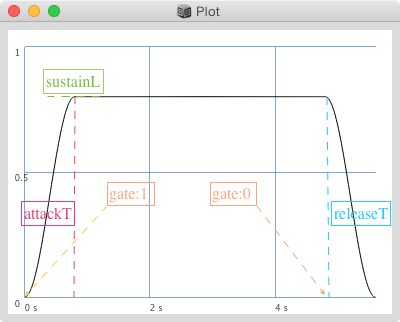
// attacco sostegno rilascio curva
Env.asr(0.08, 1, 2, \sin).test(4).plot;
(
SynthDef(\asr,
{arg freq=890, gate=0, a=0.1, r=0.6, amp=0, done=2;
var sig,env;
sig = SinOsc.ar(freq);
env = Env.asr(a,amp,r,-4);
env = EnvGen.kr(env,gate,doneAction:done);
sig = sig * env;
Out.ar(0, sig)
}
).add;
)
a = Synth(\asr, [\amp,0.5]);
a.set(\gate,1);
a.set(\gate,0);
Env.adsr - il più classico degli inviluppi.
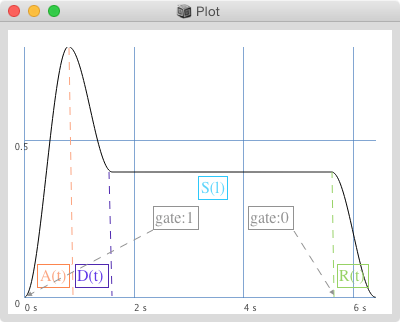
// attacco decadimento sostegno rilascio curva
Env.adsr(0.08, 0.1, 0.5, 2, curve:\sin).test(4).plot;
(
SynthDef(\adsr,
{arg freq=890, gate=0, a=0.1, d= 0.1, s=0.5, r=0.6, amp=0, done=0;
var sig,env;
sig = SinOsc.ar(freq);
env = Env.adsr(a,d,s,r);
env = EnvGen.kr(env,gate,doneAction:done);
sig = sig * env * amp;
Out.ar(0, sig)
}
).add;
)
a = Synth(\adsr, [\amp,0.5]);
a.set(\gate,1);
a.set(\gate,0);
Env.circle - inviluppo in loop - l'array dei tempi delta deve contenere lo stesso numero di elementi di quello dei livelli.
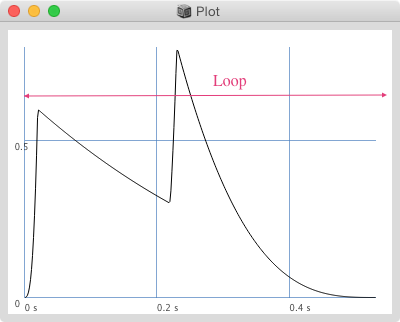
// livelli tempi curva
Env.circle([0.0, 0.6,0.3, 0.8,0.0], [0.02,0.2,0.01,0.3,0.2], \cub).plot;
(
SynthDef(\circle,
{arg freq=890, gate=0, amp=0;
var sig,env;
sig = SinOsc.ar(freq);
env = Env.circle([0.0, 0.3, 0.1, 0.5, 0.0 ],
[ 0.02, 0.2, 0.01, 0.3,0.2],\cub);
env = EnvGen.kr(env,gate);
sig = sig * env * amp;
Out.ar(0, sig)
}
).add;
)
a = Synth(\circle, [\amp,0.5]);
a.set(\gate,1);
a.set(\gate,0);
Fades¶
In alcune situazioni potremmo dover generare un fade in e un fade out automatico alla creazione e/o distruzione di un'istanza di ___Synth___ per evitare clicks dovuti a eventuali discontinuità del segnale.
In SuperCollider possiamo farlo in due modi.
- Linen.kr - come Env.asr ma sotto forma di UGen - più pratico ma solo con rampe lineari.
(
SynthDef(\linen,
{arg freq=890, gate=0, a=0.1, r=0.6, amp=0, done=2;
var sig,env;
sig = SinOsc.ar(freq);
env = Linen.kr(gate, a, amp, r, done);
sig = sig * env;
Out.ar(0, sig)
}
).add;
)
a = Synth(\linen, [\amp,0.5]);
a.set(\gate,1);
a.set(\gate,0);
- XLine.kr e Env.cutoff - rampe non lineari.
(
SynthDef(\fades,
{arg freq=890, gate=1, fin=1, fout=1, amp=0, done=2; // gate=1
var sig, fdIn, fdOut;
sig = SinOsc.ar(freq);
fdIn = XLine.kr(0.001,amp, fin);
fdOut = Env.cutoff(fout, amp, \sin);
fdOut = EnvGen.kr(fdOut,gate,doneAction:done);
sig = sig * fdIn * fdOut;
Out.ar(0, sig)
}
).add;
)
a = Synth(\fades, [\amp,0.5]);
a.set(\gate,0);
Pure Data¶
In PD possiamo costruire inviluppi con fase di sostegno in due modi.
Flag¶
- Definiamo l'inviluppo
- Specifichiamo il flag -suspoint nell'oggetto else/envgen~ (il numero del punto di sostegno)
- Un valore > 0 $\rightarrow$ gate 1 (note on)
- Un valore < 0 $\rightarrow$ gate 0 (note off)
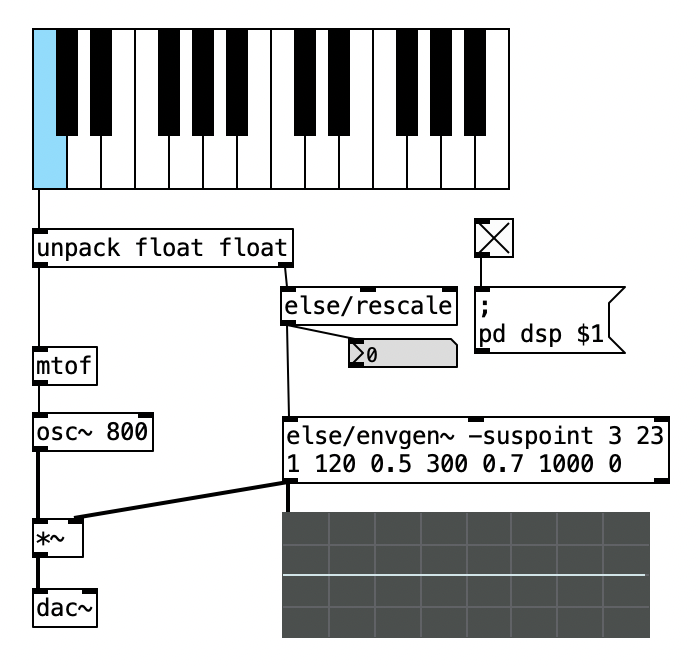
os.system('open 6_ampiezza/patch/6.8.pd')
0
adsr~¶
Oggetti dedicati come l'oggetto adsr~ dalla libreria else genera il più classico degli inviluppi d'ampiezza.
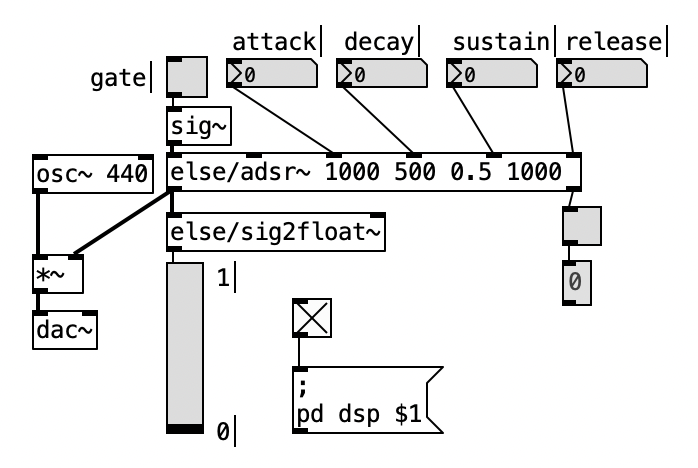
os.system('open 6_ampiezza/patch/6.9.pd')
0