Parametri del suono e forme d'onda classiche¶

Indice¶

Parametri del suono
- Altezza
- Intensità
- Fase
- Timbro
Forme d'onda classiche
- Oscillatori in SuperCollider
- Oscillatori in Max

Parametri del suono ¶

Altezza o frequenza ¶

L’altezza (o frequenza) di un suono è il parametro legato alla sensazione di gravità/acutezza che si percepisce e dipende dalle frequenze di variazione delle onde elementari che compongono l’onda sonora.

Possiamo specificare questo parametro in tre diversi tipi di notazione simbolica:

Simboli musicali - determinano l'altezza in base alla posizione grafica in un contesto di linguaggio codificato (la scrittura musicale).
Simboli alfabetici - determinano l'altezza come nomi di una scala o un modo.
Simboli numerici - in questo caso per quanto riguarda i contenuti di questo scritto possiamo fare un'ulteriore suddivisione in due diverse unità:
- MIDI Note - determinano l'altezza come valori numerici 60 = Do centrale.
  
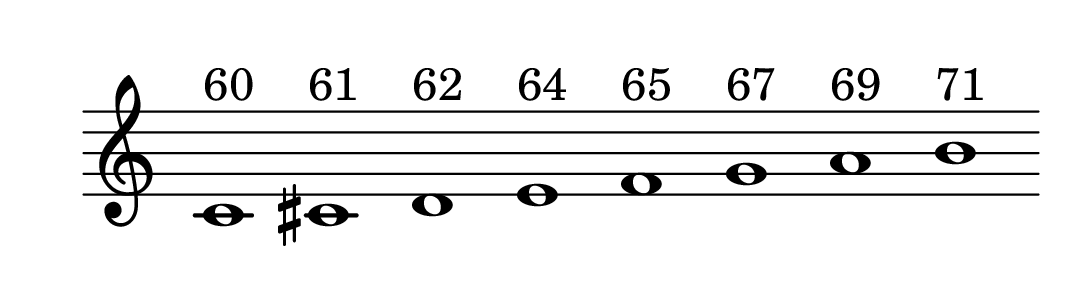
  Oltre ai valori midi esistono altre rappresentazioni simboliche assolute impiegate:
  1. Numerazione MIDI.
  2. Numerazione a Ottave (Giapponese, Yamaha, Encore).
  3. Numerazione a Ottave (Scientifica, MusicXML ed altre).
  4. Numerazione di Helmholtz (utilizzata comunemente negli Stati Uniti).
  5. Numerazione Esadecimale.
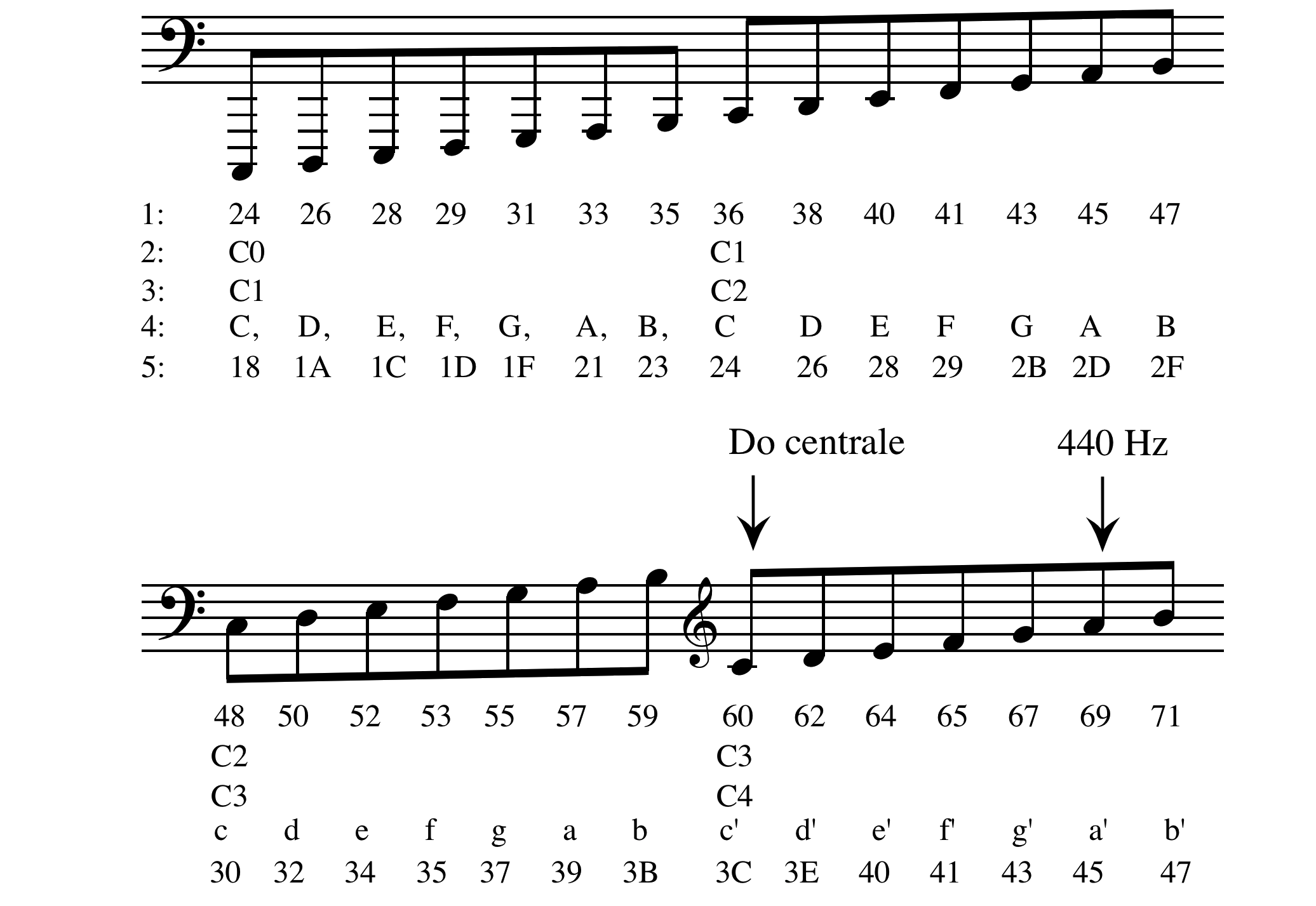
- Frequenze (Hertz) - determinano l'altezza come valori numerici che rappresentano il numero di cicli per secondo di un'onda periodica o ciclica.

No description has been provided for this image

Un'onda periodica è data da un fenomeno vibratorio che si ripete identico a se stesso a intervalli di tempo uguali.

se il singolo intervallo viene misurato nel tempo è chiamato periodo (o ciclo) dell'onda e rappresentato dalla lettera T.
se il singolo intervallo viene misurato nello spazio è chiamato lunghezza dell'onda e rappresentato dalla lettera $\lambda$ - lambda.

Possiamo rappresentare graficamente un onda attraverso un sistema di riferimento cartesiano:

asse delle ascisse (x) = scorrere del tempo
asse delle ordinate (y) = variazioni di pressione atmosferica

La frequenza di un suono periodico è misurata in Hertz o cps (cicli per secondo) ovvero si misura quante volte il periodo si ripete uguale in un secondo.

In [2]:

import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

freq  = 4# Frequenza (Hz o cps)

par.sine(freq)

L'orecchio umano nelle sue condizioni ottimali percepisce suoni compresi tra 20 e 20.000 Hz.

Nella seguente tabella i rapporti tra alcune unità di misura appena esposte.

Nota	MIDI	Rapporto	Frequenza (Hz)
Do	60	$1:1$	261.6
Do# o Reb	61	$\sqrt[12]{2}$	277.2
Re	62	$\sqrt[12]{2^2}$	293.7
Re# o Mib	63	$\sqrt[12]{2^3}$	311.1
Mi	64	$\sqrt[12]{2^4}$	329.6
Fa	65	$\sqrt[12]{2^5}$	349.2
Fa# o Solb	66	$\sqrt[12]{2^6}$	370.0
Sol	67	$\sqrt[12]{2^7}$	390.0
Sol# o Lab	68	$\sqrt[12]{2^8}$	415.3
La	69	$\sqrt[12]{2^9}$	440.0
La# o Sib	70	$\sqrt[12]{2^{10}}$	466.2
Si	71	$\sqrt[12]{2^{11}}$	493.9
Do	72	$2:1$	523.3

Intensità o ampiezza ¶

Questo parametro in termini musicali è dato dal rapporto tra i suoni più deboli (pianissimissimo) e quelli più forti che caratterizzano la dinamica di un brano.

L'intensità di un suono in fisica si definisce con il termine ampiezza in quanto descrive l’ampiezza delle variazioni dell’onda sonora rispetto allo stato di quiete e fornisce una misura dell’energia da essa trasportata.

Se prendiamo in considerazione l'aspetto fisico acustico e non la percezione umana questo parametro è indipendente dalla frequenza e per convenzione rappresentato da valori compresi tra -1.0 e +1.0 e che nell'audio digitale corrisponde al valore del singolo campione.

In [10]:

import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

freq  = 8         # Frequenza (Hz o cps)
amp   = 0.2       # Ampiezza (tra 0.0 e 1.0)

par.vsine(freq, amp) 
par.sine(freq, amp)

Fase e moto armonico ¶

La funzione sinusoidale può rappresentare una legge oraria chiamata moto armonico semplice che è un moto periodico lungo un asse rettilineo detto origine (O).

$x(t) = a * sin(\omega t + \varphi)$

Dal punto di vista cinematico può essere visto come:

Il punto blu si muove per moto circolare uniforme sulla circonferenza, lungo il diametro.
- La sua velocità è costante.
il punto rosso è la sua proiezione sull'asse x e continua a oscillare lungo i due estremi del diametro con l'origine al centro dell'oscillazione.
- La sua velocità non è costante, è massima al centro e nulla agli estremi.
- L'accelerazione è massima agli estremi e nulla al centro.
Il punto verde è la rappresentazione nel tempo.

La massima distanza dall'origine è l'Ampiezza del moto e va da -1 a +1.
la durata di un'oscillazione completa rispetto l'origine è il Periodo e corrisponde a $2\pi$ (360°).
L'origine dell'oscillazione è la sua Fase.

In [5]:

import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

freq = 5    # Cambia i parametri...
amp  = 1
fase = 0.5 

par.sinepar(freq,amp,fase)

Timbro ¶

Il timbro è quella particolare qualità del suono che permette di distinguere due suoni con uguale ampiezza e altezza e consente all'ascoltatore di identificare la fonte sonora, rendendola distinguibile da ogni altra.

Il timbro dei suoni naturali è influenzato da moltissimi parametri variabili come ad esempio le caratteristiche fisiche dei materiali della sorgente sonora e dal modo in cui è messo in vibrazione.

Tutti questi parametri concorrono a formare una rappresentazione fisica del timbro di quel suono ovvero la sua forma d'onda, che descrive come varia nel tempo la pressione atmosferica (o il voltaggio di un segnale) nel produrre quel determinato suono.

Nelle celle sottostanti sono illustrate tre diverse forme d'onda:

suono puro - è formato da una sola onda sinusoidale con propria frequenza, ampiezza e fase. Non esiste in natura e può solo essere sintetizzato

In [9]:

import os
import sys
import IPython.display as ipd
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

par.puro()
ipd.Audio('4_parametri/media/puro.mp3')

Out[9]:

suono complesso periodico - è caratterizzato dalla presenza di più sinusoidi (suoni parziali) sovrapposte, ognuna con una propria frequenza, una propria ampiezza e una propria fase che hanno un qualche tipo di relazione tra loro.

In [13]:

par.periodico()
ipd.Audio('4_parametri/media/periodico.mp3')

Out[13]:

suono complesso aperiodico (rumore) - come il precedente ma i parametri non sono in relazione tra loro.

In [15]:

par.noise()
ipd.Audio('4_parametri/media/noise.mp3')

Out[15]:

Gli elementi principali che contribuiscono alla caratterizzazione delle forme d'onda sono due:

nel dominio della frequenza le componenti spettrali
nel dominio del tempo l'inviluppo spettrale

I suoni presenti in natura non producono mai suoni puri (onde sinusoidali perfette) ma sono caratterizzati da forme d'onda differenti tra loro e dunque da suoni complessi.

Un suono complesso è il risultato della sovrapposizione (somma) di più suoni puri ognuno con frequenza, ampiezza e fase differenti secondo il teorema enunciato dal fisico francese J.Fourier nei primi anni dell'800:

Qualunque segnale periodico può essere scomposto nella somma di un eventuale termine costante e di segni sinusoidali, dei quali il primo, avente lo stesso periodo e quindi la stessa frequenza del segnale considerato, si chiama prima armonica o fondamentale, e gli altri, aventi periodi sottomultipli e quindi frequenze multiple, si chiamano armoniche superiori

In [17]:

import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

par.fourier()

Per chiarire ulteriormente possiamo pensare uno spettro sonoro come un accordo musicale le cui singole note sono eseguite da suoni sinusoidali (un singolo suono puro per ogni nota) che l'orecchio umano non percepisce come un accordo formato da più note ma come un singolo suono con un determinato timbro.

Ogni suono puro che concorre a formare uno spettro complesso può essere chiamato suono armonico o parziale.

La differenza terminologica tra queste due definizioni è sottile e implica la conoscenza del tipo di spettro a cui si riferisce.

Fondamentalmente gli spettri sonori possono essere suddivisi in due grandi famiglie la cui differenziazione è data dai rapporti frequenziali intercorrenti tra le componenti pure che li formano.

Spettri armonici. Le frequenze dei parziali seguono rapporti formati da numeri interi:

$1:1$ - Fondamentale
$1:2$ - Primo armonico
$1:5$ - Quarto armonico
$1:8$ - Settimo armonico
...
1:n - Ennesimo armonico

I parziali possono essere chiamati anche armonici dove il suono (usualmente) più grave che corrisponde al rapporto 1:1 è chiamato fondamentale ed è quello che generalmente caratterizza l'altezza percepita di quel suono complesso, mentre i parziali successivi sono chiamati primo armonico, secondo armonico, e via dicendo fino idealmente a infinito.

La forma d'onda di questi suoni complessi può essere solamente periodica.

In questo caso, stabilita la frequenza fondamentale in Hertz per ricavare le frequenze degli armonici basterà moltiplicarne il valore per i numeri interi.

In [21]:

from IPython.display import Audio
Audio('4_parametri/media/armonico.mp3')

Out[21]:

Spettri inarmonici. Le frequenze dei parziali non seguono alcun rapporto particolare, o meglio non sono in rapporto con un suono fondamentale che è assente.

$4.0:2.5$ - Primo parziale
$1.2:8.7$ - Secondo parziale
$1.4:2.9$ - Terzo parziale
$9.3:5.2$ - Quarto parziale
...
$n:n$ - Ennesimo parziale

La forma d'onda di questi suoni può essere sia periodica che aperiodica.

In [23]:

from IPython.display import Audio
Audio('4_parametri/media/inarmonico.mp3')

Out[23]:

Possiamo affermare che tutti i suoni possibili sono formati da spettri compresi tra:

suono puro (la singola sinusoide - periodico) e
suono più complesso (il rumore bianco - aperiodico)

le cui caratteristiche oscillano tra suoni inarmonici, suoni quasi armonici e suoni armonici.

In [29]:

import os
import librosa
import IPython.display as ipd
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

sr     = 22050                                # Frequenza di campionamento
path   = os.path.abspath('4_parametri/media/tenuto.wav')  # Path file
offset = 1                                    # Offset in secondi
w_size = 1024                                 # Window size (in samples)

y, sr = librosa.load(path, sr=sr,offset=offset, duration=(1/sr)*w_size) # Assegna le ampiezze istantanee di y

par.plotFFT(y,sr,150)

ipd.Audio('4_parametri/media/tenuto.wav')

Out[29]:

Forme d'onda classiche ¶

Ci sono delle forme d'onda ormai ritenute classiche in quanto erano le sole che potevano essere generate dai primi oscillatori che sono stati costruiti.

Nel proseguio di questo scritto impiegheremo solo queste forma d'onda classiche a spettro fisso in quanto le tematiche legate alla sintesi ed elaborazione del suono sono affrontate in un altra parte del sito.

Oscillatori in SuperCollider¶

In SuperCollider ci sono generalmente due copie degli stessi oscillatori (UGens).

Una limitata in banda di frequenza che elimina il problema del foldover e può essere inviata agli output.

Osserviamo le diverse forme d'onda e le caratteristiche spettrali attraverso i monitors più adatti ai parametri che vogliamo indagare.

In [ ]:

{ SinOsc.ar(400).poll(10) }.play;  // Sinusoidale
{ Saw.ar(400) }.play;              // Dente di sega
{ Pulse.ar(400) }.play;            // Onda quadra
{ VarSaw.ar(400) }.play;           // Onda triangolare
{ Blip.ar(400) }.play;             // Treno d'impulsi

{ WhiteNoise.ar }.play;            // Rumore bianco
{ PinkNoise.ar }.play;             // Rumore Rosa
{ BrownNoise.ar }.play;            // Rumore Browniano
{ GrayNoise.ar }.play;             // Rumore grigio
{ ClipNoise.ar }.play;             // Rumore clippato

Una con la forma d'onda pura non limitata in banda di frequenza che possiamo utilizzare come segnale di controllo ovvero per controllare i parametri di qualche altra UGen. Generalmente è preceduta dal suffizzo ___LFNome_dell_oscillatore___ (LF sta per Low Frequency). Possiamo inviarla agli outputs ma dobbiamo controllare il fenomeno del foldover.

In [ ]:

{ LFPar.ar(400).poll(10) }.play;  // Sinusoidale (parabolica)
{ LFSaw.ar(400) }.play;           // Dente di sega
{ LFPulse.ar(400) }.play;         // Onda quadra
{ LFTri.ar(400) }.play;           // Onda triangolare
{ Impulse.ar(400) }.play;         // Treno d'impulsi

{ LFNoise0.ar }.scope;            // Generatori random
{ LFNoise1.ar }.scope; 
{ LFNoise2.ar }.scope; 
{ LFClipNoise.ar }.scope;

Alcuni paragoni visivi (plot).

In [ ]:

(
{[SinOsc.ar,     // Oscillatore sinusoidale
  WhiteNoise.ar, // Generatore di rumore bianco
  Saw.ar,        // Generatore di onde a dente di sega
  Pulse.ar,      // Generatore di onde quadre
  Blip.ar,       // Treno d'impulsi (PulseTrain)

  LFPar.ar,      // Parabolica (Quasi-Sine)
  LFNoise0.ar,   // Generatore di valori pseudo-casuali
  LFSaw.ar,
  LFPulse.ar,
  Impulse.ar]
}.plot(1/70, minval:-1, maxval:1);
)

Oscillatori in PD Indice

In PD abbiamo degli oggetti delle diverse librerie che sono simili a qualli di di Max per la generazione di onde classiche.

I parametri che corrispondono agli argomenti delle UGens in SuperCollider sono inviati attraverso GUI negli inlets degli oggetti oppure specificati come argomenti di default al momento della creazione degli oggetti stessi.

Per conoscere quali sono i parametri che possiamo controllare dobbiamo consultare l'Help file del singolo oggetto.

In [35]:

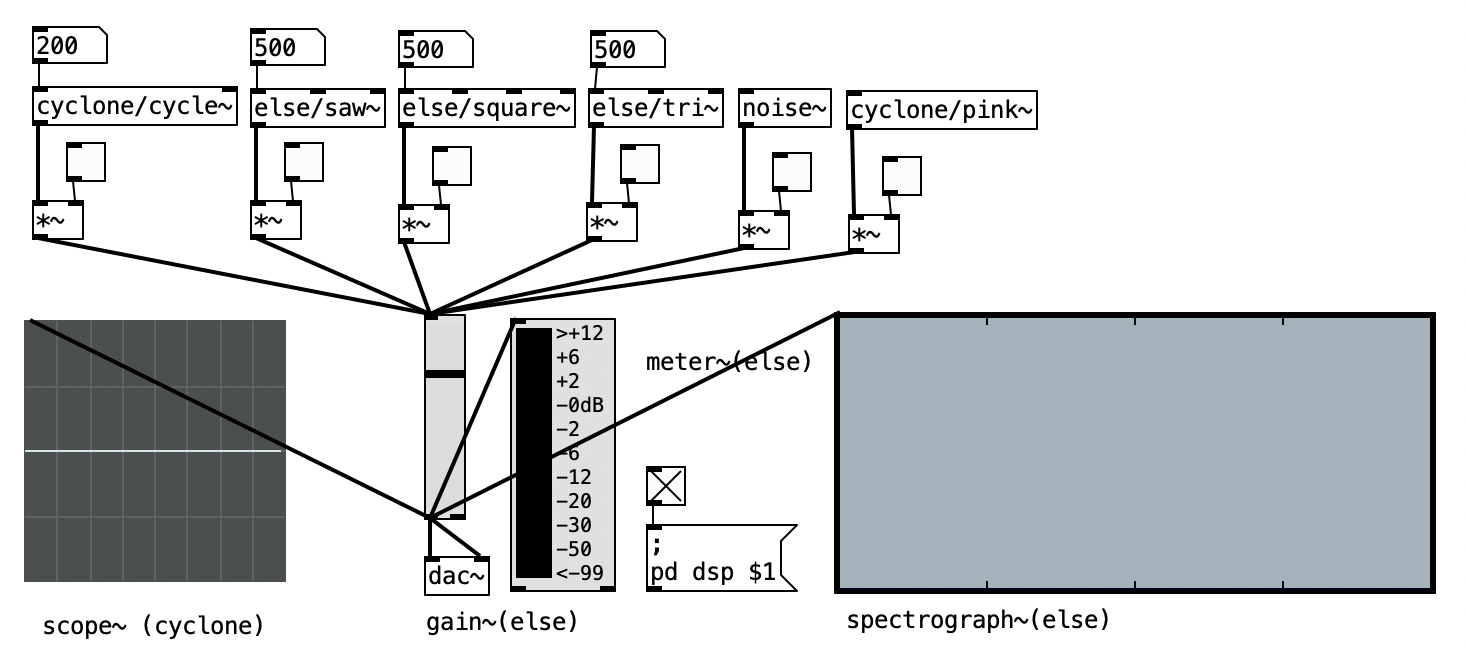
os.system('open 4_parametri/patch/4.1.pd')

Out[35]:

Parametri del suono e forme d'onda classiche¶

Indice¶