Segnali audio¶
Indice¶
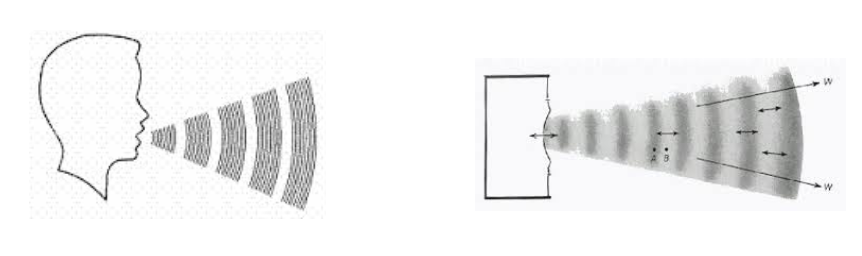
In fisica un’onda è una perturbazione che si propaga nello spazio e che può trasportare energia da un punto all’altro.
Per produrre suono la sorgente sonora deve essere immersa all’interno di un mezzo elastico che solitamente ma non necessariamente è l’aria.
Quando un'onda viaggia in un mezzo elestico la sostanza di questo mezzo è temporaneamente deformata.
Le onde sonore si propagano attraverso collisioni tra molecole vicine.
Dopo la collisione le molecole tornano indietro in direzione opposta, oscillando intorno ad una posizione quasi fissa.
Le onde sonore sono onde meccaniche longitudinali in quanto le oscillazioni sono parallele alla direzione della propagazione.
Rappresentazione nel dominio del tempo
- piano cartesiano
- *assi ruotati di 90° rispetto al video.
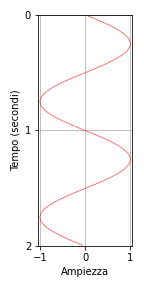
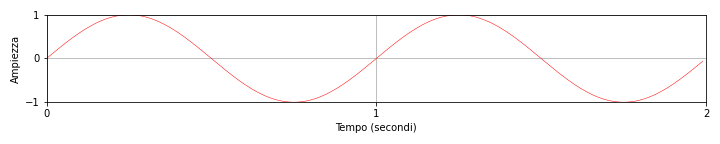
- ascisse (x) $\rightarrow$ tempo
- ordinate (y) $\rightarrow$ ampiezza
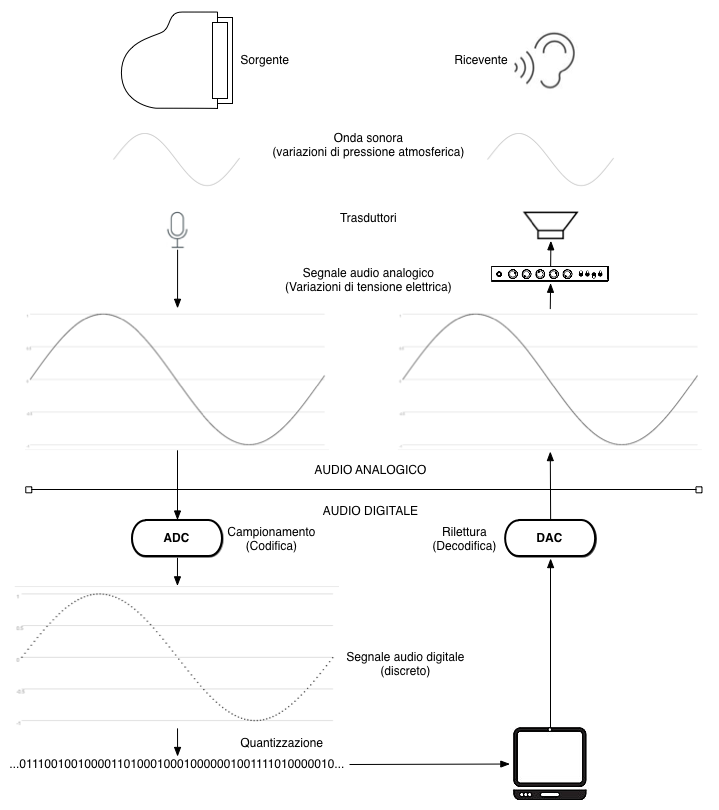
Nel corso del suo tragitto all’interno del corpo vibrante un’onda sonora può incontrare un apparato in grado di trasformare (ed eventualmente elaborare) l’energia sonora in energia di altra forma.
il sistema uditivo umano ad esempio trasforma le variazioni di pressione atmosferica in impulsi nervosi che sono interpretati dal cervello come sensazione uditiva.
un qualsiasi tipo di microfono trasforma le variazioni di pressione atmosferica in variazioni di tensione elettrica che scorre all’interno di un sistema elettroacustico analogico.

Segnale analogico ¶
I microfoni trasducono l'energia meccanica propria delle onde sonore in energia elettrica utilizzando diverse tecnologie (induzione elettromagnetica, induzione elettrostatica o piezoelettricità).
L'energia elettrica generata (corrente alternata) scorre nel cavo collegato al microfono e il suo andamento segue in modo analogo l'andamento delle variazioni di pressione originali trasportando l'informazione attraverso tutti i dispositivi connessi tra loro all'interno di una catena elettroacustica.
Questo tipo di segnale è continuo sia nel tempo che in ampiezza.
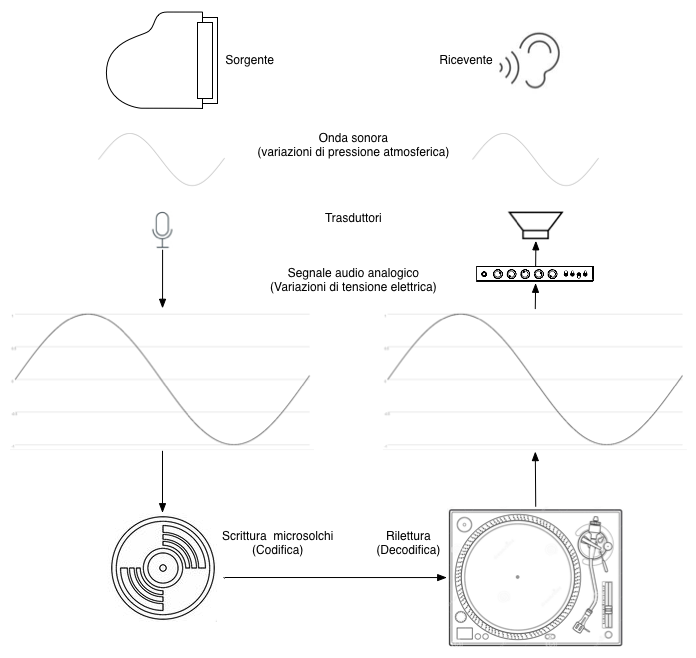
Segnale digitale ¶
Possiamo pensare l'audio digitale come un prolungamento della catena elettroacustica analogica in quanto il processo di campionamento o digitalizzazione consiste nel misurare a precisi istanti di tempo separati tra loro da un tempo delta costante (chiamato periodo di campionamento) l'ampiezza del segnale analogico espressa sotto forma di tensione elettrica.
Il range di riferimento dei valori è compreso tra +1.0 e -1.0
La singola misura è chiamata campione (sample) e dopo aver subito un processo di quantizzazione produce una sequenza di parole binarie che corrispondono all’andamento del segnale.
Questo tipo di segnale è discreto sia nel tempo che in ampiezza.
Segnale campionato ¶
Campionare un segnale significa dunque misurarne l'ampiezza (y) a ogni periodo di campionamento
- quanto deve durare un periodo?
Più è breve minore sarà la perdita di informazioni tra un campione e il successivo.
### import numpy as np
import os
import sys
sys.path.insert(0, os.path.abspath('moduli'))
import campiona as cmp
%matplotlib inline
periodo = 0.02 # (secondi) Modifica il periodo
cmp.img(1/periodo)
Ci sono però limiti tecnologici nella costruzione dei convertitori ADC che non ci permettono di arrivare a periodi così brevi.
Partiamo allora dal presupposto che i campioni devono essere misurati a una frequenza dipendente dalla frequenza del segnale da campionare.
Siccome secondo il teorema di Fourier tutti i suoni possono essere scomposti come somma di sinusoidi ognuna delle quali con frequenza, ampiezza e fase proprie il periodo di campionamento è determinato dalla componente armonica con frequenza più alta.

Le frequenze dei parziali di uno spettro sono espresse in Hertz ovvero in cicli per secondo (cps), conviene allora uniformare l'unità di misura sostituendo il periodo di campionamento con la rata di campionamento (Sample rate o sr o Audio rate) che è anch'essa espressa in Hertz e ci dice quanti campioni sono misurati in un secondo.
Quanto più alta sarà la frequenza di campionamento, tanto più accurata sarà la descrizione del segnale.
Basta far coincidere la frequenza del parziale più alto del suono da campionare con la rata di campionamento per ottenere un'informazione corretta?
No.
Sono necessari almeno due campioni per periodo del segnale o meglio: la frequenza di campionamento deve essere almeno il doppio della frequenza massima presente nello spettro del segnale (frequenza di Nyquist).
import numpy as np
import os
import sys
sys.path.insert(0, os.path.abspath('moduli'))
import rata as rt
%matplotlib inline
freq = 12 # Frequenza sinusoide (Hz)
spc = 20 # Numero di campioni per ciclo (Hz)
# freq 12 spc 1 = Nessun suono (0)
# freq 12 spc 1.2 = Aliasing (suono con pitch più basso)
# freq 5 spc 2 = Minima rata di campionamento
rt.img(freq,spc)
Teorema di Nyquist-Shannon - se non adottato come regola porta alla generazione di errori dati dal fenomeno dell'aliasing o foldover
import numpy as np
import os
import sys
sys.path.insert(0, os.path.abspath('moduli'))
import rata as rt
%matplotlib inline
freq = 12 # Frequenza sinusoide (Hz)
spc = 2 # Numero di campioni per ciclo (Hz)
# freq 12 spc 1 = Nessun suono (0)
# freq 12 spc 1.2 = Aliasing (suono con pitch più basso)
# freq 5 spc 2 = Minima rata di campionamento
rt.img(freq,spc)
Le possibili soluzioni sono due:
Utilizzare la più alta frequenza di campionamento possibile innalzando di fatto la frequenza di Nyquist oltre la soglia dell'udibilità umana (20.000Hz)
Inserire un filtro passa-basso (anti aliasing) sia prima del campionamento che dopo la rilettura (per compensare eventuali modifiche delle fasi operate dal filtro in ingresso).
La rata di campionamento dello standard CD è stata fissata nel 1982 a 44.100 Hz proprio perchè è il doppio della soglia di udibilità umana (20.000 * 2) più 4.100 Hz che compensano la pendenza di taglio del filtro passa-basso in ingresso.
Ai giorni nostri quasi tutti gli hardware dedicati all'audio digitale possono arrivare a frequenze di campionamento a 48.000 e 96.000 Hz annullando di fatto qualsiasi problematica relativa alla perdita di informazioni tra campioni successivi e al fenomeno dell'aliasing.
Segnale quantizzato ¶
La trasformazione dell'ampiezza di un segnale da continua a discreta prende il nome di quantizzazione.
Ogni valore misurato dal processo di campionamento (ampiezza istantanea) deve essere associato a un nuovo valore compreso in un insieme discreto di livelli introducendo in questo modo una serie di imprecisioni chiamata errori di quantizzazione.
import numpy as np
import os
import sys
sys.path.insert(0, os.path.abspath('moduli'))
import quantuni as qntu
%matplotlib inline
bit = 2 # Numero di bit
lev = 2**bit # Numero di livelli
qntu.img(2,30,lev)
Con un numero maggiore di bit (e di conseguenza di scalini) diminuiscono gli errori di quantizzazione,
A parità di errore di quantizzazione le ampiezze più piccole in valore assoluto sono distorte maggiormente (in proporzione) rispetto a quelle più grandi.
Per ovviare a questo problema e al fatto che l'essere umano percepisce meglio le variazioni che interessano ampiezze basse è stata pensata un'altra tecnica di quantizzazione non uniforme dove il numero di livelli di quantizzazione è diverso dagli intervalli di ampiezza del segnale originale.
Le ampiezze deboli sono spaziate meno di quelle elevate e dunque quantizzate con più precisione.
Possiamo inoltre definire a seconda delle esigenze l'indice di compressione.
import numpy as np
import os
import sys
sys.path.insert(0, os.path.abspath('moduli'))
import quantmu as qntu
%matplotlib inline
mu = 255 # Indice di compressione (prova a cambiare)
qntu.img(2,30,mu,16)
Segnale numerico ¶
L'ampiezza di un segnale analogico (espressa in Volt) può essere quantificata attraverso numero appartenente a un sistema decimale.
L'ampiezza di un segnale digitale deve essere quantificata attraverso un sistema binario in quanto tutti i sistemi digitali accettano solo due stati:
- 0 = circuito aperto = falso
- 1 = circuito chiuso = vero
Sistema binario $\rightarrow$ numeri espressi in parole di diversa lunghezza
Ogni singolo elemento è chiamato cifra significativa o in termini informatici bit (binary digit).
Il bit è la più piccola unità d'informazione manipolabile da un calcolatore digitale ed è possibile rappresentare fisicamente questa informazione con un segnale elettrico o magnetico che se supera una determinata soglia corrisponde al valore 1 altrimenti al valore 0.
Appare evidente come gli scalini illustrati nel paragrafo precedente corrispondano al numero di bit con i quali rappresentiamo un valore di ampiezza.
Con un bit possiamo ottenere due soli valori ( $2^1$ ):
| Valore binario | Valore decimale |
|---|---|
| 0 | 0 |
| 1 | 1 |
Con due bit quattro valori diversi ( $2^2$ )
| Valore binario | Valore decimale |
|---|---|
| 00 | 0 |
| 01 | 1 |
| 10 | 2 |
| 11 | 3 |
Con tre bit otto valori diversi ( $2^3 $)
| Valore binario | Valore decimale |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
E via dicendo, per un gruppo di n bit possiamo rappresentare $2^n$ valori.
Infine facciamo un esempio della quantizzazione di un segnale analogico compreso tra +/- 5V con una profondità di 8 bit:
| Valore di tensione | Valore binario |
|---|---|
| [-5.000, -4.961] | 00000000 |
| [-4.961, -4.922] | 00000001 |
| [-4.922, -4.883] | 00000010 |
| [-4.883, -4.844] | 00000011 |
| ... | 00000100 |
| ... | ... |
| ... | ... |
| ... | 11111011 |
| [+4,844, +4,883] | 11111100 |
| [+4,883, +4,922] | 11111101 |
| [+4,922, +4,961] | 11111110 |
| [+4,961, +5,000] | 11111111 |
In questo caso abbiamo una precisione del segnale che è data da: $10/2^8 V = 10/256 V = 0,039 V$ e tutti i valori di tensione compresi in un intervallo di $0,039V$ sono rappresentati dallo stesso valore.
In informatica ci sono unità di informazioni che sono caratterizzate dal numero di bit che le descrivono ad esempio il byte è composto da 8 bit e permette di memorizzare un carattere (char) o una cifra (int) compresa tra 0 (00000000) e 255 (11111111).
Questo raggruppamento di numeri permette una migliore leggibilità come quando in base decimale raggruppiamo un numero a tre per poter distinguere le migliaia (il numero 1.256.245 è decisamente più leggibile che 1256245).
Un'altra unità di informazione composta da 16 bit è chiamata parola (word) mentre un'informazione a 32 bit parola doppia (double word).
Dal Dicembre 1998 l'organismo internazionale IEC (International Electrotechnical Commission) ha standardizzato alcune unità di misura informatiche:
- Kilobite (KB) = 1000 byte - prima del 1998 era 210 = 1024 byte.
- Megabite (MB) = 1000 KB = 1.000.000 byte - prima del 1998 era 220 = 1024 KB = 1.048.576 byte.
- Gigabite (GB) = 1000 MB = 1.000.000.000 byte - prima del 1998 era 230 = 1024 MB = 1.073.741.824 byte.
- Terabite (TB) = 1000 GB = 1.000.000.000.000 byte - prima del 1998 era 240 = 1024 GB = 1.099.511.627.776 byte.
Conoscendo la frequenza di campionamento in Hertz ($Fc$), la profondità di quantizzazione in bit ($N$) e la durata del flusso audio in secondi ($D$) possiamo stabilire quanti bit abbiamo bisogno per memorizzare un segnale digitale monofonico non compresso:
$$Size = Fc * N * D$$Il numero di bit compreso nell'unità di tempo (un secondo) si chiama bit rate e si misura in bps (bit per secondo) oppure KBps (KiloByte per secondo).
$$bitrate (bps) = Fc * N * nchan$$$$bitrate (KBps) = Fc * N * nchan / 8$$| Supporto | Fc (Hz) | Bit | Canali | Bit rate (KBps) | |
|---|---|---|---|---|---|
| Telefono | 8.000 | 8 | 1 | 8.00 | |
| Radio AM | 11.025 | 8 | 1 | 11.05 | |
| Radio FM | 22.050 | 16 | 2 | 88.20 | |
| CD Audio | 44.100 | 16 | 2 | 176.40 | |
| DAT | 48.000 | 16 | 2 | 192.00 | |
| DVD Audio | 192.000 | 24 | 6 | 1200.00 |